Il sole, un teodolite
distanziometrico, un cellulare, la necessaria scrupolosità,
e il Nord geografico è
mio!
di Sandro Angei
Sommario
Scopo di questo studio è quello di verificare se esista un metodo relativamente facile, affidabile e abbastanza preciso di misurazione, per l'individuazione dell'orientamento di un manufatto rispetto al nord geografico. Un metodo che faccia a meno della bussola (poco precisa), di rilievi topografici in appoggio a punti trigonometrici IGM (ossia una rete nazionale di appoggio), e che faccia a meno degli strumenti topografici di ultima generazione denominati GPS, legati ad apparati globali (costellazione di satelliti artificiali). Un metodo che sia alla portata di tutti, o quasi. Il metodo esiste e fà uso, in combinazione con altri, di uno strumento (il telefono cellulare) che da qualche anno ormai, essendo collegato ad internet, fornisce l'ora esatta... molto esatta.
Avvertenza
Come appena scritto nel sommario, questo articolo tratta della misura di azimut riferiti al nord geografico. Non volendo ogni volta dover specificare che di questi azimut, e solo di questi, stiamo trattando, quando in taluni contesti scriverò ad esempio: "individuazione del nord geografico" (con "nord geografico" in corsivo) intenderò sempre "azimut riferiti al nord geografico"; perché di fatto in questi studi non ha alcuna utilità individuare materialmente la direzione del nord geografico.
Introduzione
Il presente studio è finalizzato alla individuazione dell'orientamento di un edificio rispetto al nord geografico, allo scopo di entrare, tramite l'elaborazione di un modello tridimensionale dell'edificio, nell'intima natura della ierofania luminosa che in esso si manifesta.
Per fare ciò è necessario individuare con esattezza la direzione del nord geografico.
Più in generale il metodo potrà servire ogni qualvolta sia necessario orientare un edificio o un monumento, qualsiasi motivo lo imponga.
L'individuazione
della direzione del nord geografico gran pena ha fatto patire, fin
dalla notte dei tempi, a naviganti ed esploratori di tutto il
mondo. La bussola fu di certo una conquista importantissima, capace di definire con una certa approssimazione la direzione del
nord geografico attraverso quella del nord magnetico; purtroppo però, quest'ultimo, non coincide esattamente col primo, se non in due meridiani
contrapposti, lungo i quali il polo nord magnetico giace in un dato
periodo temporale1.
Per tanto per ottenere la direzione del nord geografico è necessario
apportare una correzione a quello magnetico, definita "declinazione magnetica".
La bussola però può essere influenzata da anomalie magnetiche
locali, che possono deviare anche di decine di gradi la direzione
segnata dall'ago (e qualcosa ne sanno certi
archeoastronomi). In ogni caso la precisione di questo congegno non
supera quella di un grado.
Un altro modo per
definire il nord geografico è quello di riferirsi, di notte, alla
posizione della stella polare ma , ahimé, anche questa non è precisissima, avendo una declinazione in data corrente di 89.3481° ossia 0°39'07" dal nord geografico. Di giorno un metodo è quello di utilizzare le ombre del sole in due momenti equidistanti
a cavallo del passaggio in meridiano della nostra stella; e questo
senza dover far uso di particolari e sofisticati congegni, basta
un'asta posta perfettamente verticale col filo a piombo, un
rudimentale compasso e tanta pazienza. Di certo il metodo non può
essere utilizzato per definire l'orientamento rispetto al nord geografico di
una linea esterna al congegno, ma serve solo per indicare la
direzione del nord geografico. Direzione, però, che con gli
opportuni accorgimenti può essere di ottima precisione, e questo
trasparirà dalla trattazione che qui faremo su un metodo ibrido, che
può essere utilizzato per misurare angolarmente in modo molto
preciso la direzione di una linea d'ombra qualsiasi, della quale si vuol
conoscere l'azimut rispetto al nord geografico. Metodo che fa uso
dell'ombra proiettata dal sole in un preciso momento e della
registrazione dell'ora esatta in quel dato momento.
**
Quando mi affacciai al
mondo dell'archeoastronomia, mi resi conto che proprio per questi
temi è necessaria la precisa individuazione del nord geografico,
pena l'inconsistenza di certe ipotesi di lavoro.
Da topografo ho sempre
dato il giusto peso all'aspetto topografico del tema
archeoastronomico, e malgrado le difficoltà, gran perizia ho sempre
usato nella individuazione del nord geografico a costo, a volte, di
grande impegno. Per tanto la scoperta di un modo “semplice” di
rilevare azimut riferiti al nord geografico, gran sollievo darebbe a me, ma più in
generale a tutti gli archeoastronomi; per lo meno quelli che possono
dotarsi di un teodolite distanziometrico. Per tanto, via bussole e stella polare o
quant'altro; via anche Google Earth, almeno per questo specifico scopo. Il programma di Google sarà però, come vederemo, validissimo ausilio per la definizione del nord geografico qui trattato, nonché per una verifica, che non guasta mai. In ogni caso
Google Earth continueremo ad usarlo anche per altri scopi, vista la sua
affidabilità; ma non mi dilungherò di certo in questo tema che
esula dai fini di questo studio.
**
E' da un po' di tempo
che uso questo metodo, ma non mi decidevo a condividerlo con altri,
non per gelosia, per carità! Non sarei qui a spiegarne i dettagli; ma semplice inerzia dettata dalla difficoltà di esporre nei minimi particolari tutta la procedura. Procedura che per certi aspetti fa parte della mia esperienza di topografo, ma certi passaggi investono tematiche aliene a questo campo; in particolar modo quella relativa alle ombre. La stessa tematica, quella delle ombre, che ha indotto altri ricercatori (che citerò più in là) a sottovalutare la precisa individuazione dell'ombra, dal momento che entrare nel merito del problema comporta quella sperimentazione che và al di là dell'aspetto professionale del topografo. Per tanto non avendo, loro, la necessaria spinta emotiva e, probabilmente, alcun obiettivo pratico da perseguire, hanno rinunciato a scavare in fondo al problema, si sono fermati a metà strada, pur avendo gli strumenti adatti al tema qui trattato. Io l'obiettivo c'è l'ho, la spinta emotiva pure. Le riflessioni sul tema però comportano dispendio di energie e tempo. Quel "rimuginare" sul problema che ha il sapore del "rimandare". E, rimanda oggi, rimanda domani sono passati
quasi due anni.
Ma veniamo al tema
trattato.
**
Tutta la prassi operativa che seguirà è finalizzata alla
individuazione dell'orientamento di un manufatto del quale ci
interessa conoscere la sua precisa direzione rispetto al nord geografico.
Un metodo, che in special modo in campo archeoastronomico (che è il
contesto che più ci interessa), risulta di grande utilità e
interesse perché di grande precisione; non è assoggettato a
bussole magnetiche più o meno tarate (comunque non soddisfacenti
quanto a precisione angolare); non è assoggettato a rilievi
topografici complessi e lunghi se si fa uso del teodolite; non è
assoggettato, altresì, all'uso del GPS, né al rilevamento estremamente
comodo ma relativamente impreciso delle immagini satellitari di
Google Earth.
Ad ognuno il suo
Nel 2010 fu
pubblicato su internet un articolo: “Tracciare il Nord
geografico con metodi empirici antichi e moderni - (Tracing the
geographical North with empirical methods, ancients and modern)”2
a firma dell'Ing. Giorgio Demontis e dei Geom. Filippo Contini e
Roberto Defendente.
Un articolo che affronta l'argomento ben prima di quanto
abbia fatto io (2010).
L'articolo, come si evince già dal titolo tratta le problematiche
relative al tracciamento del nord geografico con mezzi empirici.
In sostanza lo scopo di quello studio è quello di verificare quale attendibilità possa avere un metodo antico o moderno, ma empirico, nella definizione del nord geografico. Tant'è che gli autori in uno dei metodi utilizzano la direzione della parete di un edificio per calcolare tramite Google Earth la direzione del nord geografico; ossia esattamente il contrario di ciò che qui sto perseguendo: individuare cioè, la direzione azimutale di un particolare architettonico tramite individuazione del nord geografico; che tra l'altro nel metodo qui applicato non verrà mai tracciato materialmente.In particolare in quell'articolo si descrive, tra gli altri, un'altro metodo basato sull'utilizzo di un software (progecad) col quale calcolare l'ora esatta in cui il sole passa in meridiano in un luogo di coordinate geografiche note, per poi andare sul luogo scelto, posizionare col GPS la direzione calcolata e solo dopo verificare la bontà dei calcoli del CAD con l'ombra proiettata dal sole nell'ora indicata dal CAD stesso. Ora esatta alla mano naturalmente. Un metodo, questo, che serve quasi a nulla, se non renderci edotti sulla direzione precisa del nord geografico e qualche altra applicazione.
Il metodo da me descritto sfrutta la potenzialità del software e dell'ora esatta partendo, però, dalla misurazione in loco, perché è il sole che deve indicarmi la direzione del nord geografico, non il software. Il software mi servirà solo in seguito per calcolare l'azimut di orientamento di quell'ombra mediante l'ora esatta che ho annotato nel preciso momento in cui ho registrato la posizione dell'ombra sul terreno.
In fin dei conti una
procedura, la mia, che all'antico metodo delle ombre, applica la tecnologia
avanzatissima che permette misurazioni del tempo molto precise.
Quel tempo precisissimo che ormai in tutti i cellulari
collegati al web scandisce l'ora esatta, secondo dopo secondo. Tutti
possiamo accedere all'ora esatta al minuto secondo; quel minuto secondo
che nel tempo di un calmo respiro è già passato, ma a far mente
locale su di esso, magari trattenendo il respiro, è lungo, molto
lungo. Questione di punti di vista. Quel minuto secondo - a dar ragione
ai punti di vista - è al contempo sfuggente nella frenesia di gesti
veloci, ma estremamente importante nella calma del calcolo preciso
del lento procedere del sole in cielo.
Ma
lasciamo questi pensieri che sanno di spicciola filosofia per
procedere alla spiegazione di quanto appena accennato.
Il metodo
In
sostanza si individua sul terreno la direzione dell'ombra di uno "gnomone" e nel medesimo istante si tiene nota dell'ora esatta (al
minuto secondo) di tale registrazione.
Il
metodo da me descritto, ricalca per grandi linee quello proposto
nell'articolo di Demontis, Contini e Defendente, ma se ne discosta per quanto riguarda il fine ultimo, la
procedura, l'accuratezza di rilevamento dei particolari atti a
ridurre al minimo gli errori di rilevamento; e per un software di astronomia (Stellarium) usato assieme ad un CAD per il calcolo a tavolino della direzione orientata rispetto al nord geografico. Vediamolo.
La
procedura e la cura dei dettagli3 sono, in campo archeoastronomico, di fondamentale importanza. E lo
sono tanto da dover focalizzare l'attenzione sui vari aspetti del
rilievo topografico, che nella prassi professionale in genere vengono quasi sempre elusi. Mi riferisco in particolar modo all'approssimazione
nella misura delle distanze; approssimazione che nelle moderne
stazioni totali
fornite di misuratore laser integrato è dell'ordine di 1 mm; ma nella realtà dei fatti rilascia misure con una indeterminazione di ±2 mm; e se in campo topografico e catastale sono tollerabili
indeterminazioni anche di più ampia entità, e per tanto lì accettate, per
certi rilievi in campo archeoastronomico non lo sono in modo
categorico, pena la insoddisfacente precisione che potrebbe portare
ad un nulla-di-fatto nella ricerca intrapresa.
In ragione di ciò è
necessario porre la massima attenzione nella registrazione della
sequenza ripetuta di misure per verificare il gap
tra la misura più piccola e quella più grande che, come già detto,
varia generalmente in un campo di ±2
mm rispetto alla misura reale. Per tanto una differenza che può
arrivare ad un massimo di 4 mm tra una lettura e l'altra. Quantità
che sembrerebbe piccola, o addirittura ridicola, se non fosse per le
entità in gioco. Facciamo subito un esempio (Fig. 1):
Fig.1
Se la differenza riguarda due punti A e B distanti tra loro 50 m,
rilevati da una stazione "O" posta a lato del tratto rilevato (anche a
notevole distanza), indubbiamente 2 millimetri in più o in meno su
entrambe le distanze OA e OB si ridurrebbe ad una indeterminazione
dell'angolo α
di orientamento del segmento di una quantità irrilevante (0°0'17”)4;
se però il segmento AB da rilevare è di soli 1,5 m, come nel caso
della lunghezza media utilizzabile dell'ombra proiettata da un'asta verticale, di
certo quei 2 mm di indeterminazione sulle due misure estreme OA e OB
determina un angolo α
di incertezza dell'orientamento pari a 0°09'10” 5
(32 volte più ampio). Alla luce di questo problema è necessario
adottare particolari accorgimenti che possano ridurre al minimo
l'errore di indeterminazione angolare. Nella fattispecie si deve, per
quanto possibile, posizionare lo strumento topografico in linea con
l'oggetto dei nostri studi (tratto 1-2 di Fig.2) ossia quei
particolari architettonici che definiscono la ierofania luminosa. Di
conseguenza si deve posizionare l'asta che proietta l'ombra A-B sulla
linea tra lo strumento di misura "O" e il sole; in modo tale che
l'ombra sia su questa stessa linea. Asta che, montata su treppiede,
dovrà essere posizionata perfettamente
verticale
con molta, molta cura6.
Fig. 2
Ci
si accorge subito, però, di una difficoltà di carattere operativo
dovuta all'interferenza della penombra sull'ombra proiettata
dall'asta verticale7;
questa fa si che l'ombra vera si riduca di spessore man mano che si
allontana dal piano di proiezione, per tanto è necessario stabilire
un metodo operativo capace di ovviare all'inconveniente, che di fatto
pregiudicherebbe la precisione di tutta l'operazione. Vi è inoltre
un secondo elemento di disturbo, dovuto normalmente alla imperfetta
orizzontalità e scabrosità del piano di riferimento dove l'ombra
andrà a proiettarsi nel momento della registrazione. Come ovviare a
tutto ciò? Vediamo di descrivere passo passo le operazioni:
- Il primo problema è individuare quali parti dell'asta siano più confacenti alla individuazione precisa dell'ombra. Con l'asta posizionata in verticale ho notato che il puntale di appoggio, del diametro di 10 mm, proietta un'ombra nitidissima e abbastanza sottile da poter individuare la sua mezzeria, eventualmente anche a vista. Per contro la parte sommitale genera un'ombra dai contorni che sfumano nella penombra; però ho notato che la prolunga telescopica dell'asta, di diametro ridotto (16 mm), proietta un'ombra abbastanza sottile e nitida da poter essere stimata pure a vista, benché turbata dalla penombra. Si tenga conto che da prove eseguite ho accertato che tracciando due segni paralleli su un foglio di carta, il punto medio stabilito a vista si discosta da quello reale di una quantità crescente al crescere della distanza tra i due segni estremi. In sostanza fino a distanze di 14 mm il segno tracciato a “occhio” coincide esattamente con la mezzeria: (infatti ad una distanza dei segni 12 mm la mezzeria stimata è 6 mm; alla distanza 14 m la mezzeria stimata è 7 mm; però alla distanza di 19 mm la mezzeria stimata è 10 mm da sinistra o destra; alla distanza di 32 mm, la mezzeria stimata è 17 mm). Ciò significa che l'occhio umano riesce a discriminare a vista la mezzeria di tratti relativamente brevi. Per tanto il nostro è il caso ideale per stimare, (eventualmente) a vista la mezzeria dell'ombra di un'asta del diametro di 16 mm che proietta a terra un'ombra della larghezza di circa 1 cm.
- Dopo il premuroso posizionamento in perfetta verticalità dell'asta, si adagia a terra, nelle sua prossimità, una tavola abbastanza larga e lunga da accogliere l'ombra proiettata dall'asta stessa; ovviamente la tavola si posizionerà nella direzione dove si ritiene di dover effettuare la registrazione dell'ombra. Non è necessario metterla a livello. E a rigor di logica non servirebbe neppure la tavola. Ma io la uso per comodità di tracciamento dei segni marcatori.
- Possiamo dare inizio ai lavori. E' giunto il momento di prendere in mano il cellulare che visualizza l'ora esatta nell'incessante scorrere del tempo, e nel momento in cui si tiene a mente lo scadere di un minuto secondo, con una penna si segna velocemente per prima la mezzeria dell'ombra della parte alta dell'asta, solo dopo si segnerà quella al piede dell'asta. L'operazione dovrebbe richiedere un tempo non superiore ai 2 secondi tra il primo e il secondo tratto. Tempo di cui terremo conto nel calcolo della direzione reale relativa all'orario rilevato; non tanto per effettuare una correzione, ma per dimostrare che il ritardo rientra all'interno di errori più macroscopici.
- Terminata questa delicata operazione di base, per la quale velocità e precisione sono significativi ai fini dell'affidabilità e precisione del metodo, si potrà rimuovere l'asta col treppiede e iniziare le operazioni di misurazione col teodolite distanziometrico.
- Si procede alla misurazione per coordinate polari8, secondo la normale prassi di rilevamento strumentale da stazione totale, dei due segnali che materializzano l'asse dell'ombra registrata; avendo cura di posizionare con esattezza il catarifrangente in modo da individuare in modo preciso il punto di registrazione ai fini del rilievo angolare. Come vedremo più avanti, per quanto riguarda la misura lineare, se si adotta la corretta metodologia, questa influisce molto marginalmente sull'errore di orientamento, benché l'errore di misurazione insito nel distanziometro laser sia, come già accennato, pari a ± 2 mm. In seguito si misureranno tutti i punti caratteristici del monumento che concorrono alla formazione della ierofania luminosa.
Qui finisce la prima parte del lavoro; il resto sarà eseguito a
casa, al computer con l'ausilio di due software: un CAD e Stellarium.
Il primo per la restituzione in 2D del rilievo eseguito, il secondo
per calcolare in modo preciso e veloce l'azimut dell'ombra sulla base
dell'ora di registrazione dei segni, previa impostazione delle coordinate
geografiche della stazione di rilevamento.
**
A
tal proposito vi è da precisare che le coordinate geografiche potranno essere
approssimative, per tanto saranno rilevate da Google Earth.
Per
dare una idea dell'errore commesso impostando le
coordinate geografiche con 3 metri di traslazione rispetto a quelle
reali, basti dire che l'errore azimutale rilevato con Stellarium è
di 3/10 di secondo d'arco, ossia 0,00008° sessadecimali, che
equivale ad uno scostamento di 1,45 mm a una distanza di 1000 m; per
tanto un errore insignificante. Tanto più insignificante dal momento
che l'errore di posizionamento, se si individua con pazienza il punto
di stazione su Google Earth, può essere quantificato in pochi
decimetri, tenuto conto che la risoluzione attuale del programma di
Google riesce a discriminare i 12 cm della larghezza della linea di mezzeria della carreggiata stradale. Per tanto possiamo affermare che
l'errore dovuto al posizionamento della stazione è praticamente
nullo.
Il calcolo
dell'errore
Nel loro studio, Demontis, Contini e Defendente, stimano un errore
massimo teorico nella definizione del nord geografico pari a 0,36° sessadecimali
(0°21'36” sessagesimali), la maggior parte del quale sarebbe costituito
dalla difficoltà di individuazione dell'ombra rilevata (0,29°). Salvo, poi, misurare un errore d'angolo tra due metodi diversi pari a 0°04'09". Ma il loro obiettivo, come detto, era quello di verificare quale precisione si potesse raggiungere nella definizione del nord geografico. Obiettivo fine a se stesso, non certo per calcolare la direzione di un particolare architettonico rispetto al nord geografico.
Dal punto di vista meramente pratico, il dubbio maggiore sarebbe costituito dall'errore di posizione dei segni rispetto ai bordi dell'ombra; ma come abbiamo appena dimostrato per via empirica, il dubbio non sussiste, se non in maniera estremamente marginale. Parimenti non sussiste l'incertezza dovuta allo spessore del segno tracciato, che in condizioni normali al più può essere sottile 2/10 di millimetro9 e per tanto indurrebbe l'incertezza ad un massimo di 1/10 di millimetro; inoltre, come già scritto, vi è il ritardo di tempo che intercorre tra la individuazione della seconda tacca rispetto alla prima (2 secondi), che accusa un “ritardo” angolare di 0,0058°, che sembrerebbero tanti, ma se pensiamo che il segno marcato in ritardo è posto a 1 cm dal centro del piede dell'asta, ci si rende conto che di fatto la rotazione di 0,0058° per un raggio di 15 mm equivale ad una rotazione sulla circonferenza di appena 0,0015 mm (15/10.000 di millimetro): praticamente zero. Per questo motivo ho voluto precisare in precedenza che questo segno dovrà essere posizionato solo in seconda battuta.
***
Ma veniamo al calcolo dell'errore.Dal punto di vista meramente pratico, il dubbio maggiore sarebbe costituito dall'errore di posizione dei segni rispetto ai bordi dell'ombra; ma come abbiamo appena dimostrato per via empirica, il dubbio non sussiste, se non in maniera estremamente marginale. Parimenti non sussiste l'incertezza dovuta allo spessore del segno tracciato, che in condizioni normali al più può essere sottile 2/10 di millimetro9 e per tanto indurrebbe l'incertezza ad un massimo di 1/10 di millimetro; inoltre, come già scritto, vi è il ritardo di tempo che intercorre tra la individuazione della seconda tacca rispetto alla prima (2 secondi), che accusa un “ritardo” angolare di 0,0058°, che sembrerebbero tanti, ma se pensiamo che il segno marcato in ritardo è posto a 1 cm dal centro del piede dell'asta, ci si rende conto che di fatto la rotazione di 0,0058° per un raggio di 15 mm equivale ad una rotazione sulla circonferenza di appena 0,0015 mm (15/10.000 di millimetro): praticamente zero. Per questo motivo ho voluto precisare in precedenza che questo segno dovrà essere posizionato solo in seconda battuta.
Per tanto tra queste due, l'indeterminazione maggiore è quella dello spessore del
segno apposto sulla mezzeria dell'ombra, che abbiamo detto essere
pari a 1/10 di millimetro.
In
ragione di ciò, almeno in linea teorica, nel nostro rilievo
“perfetto” dovremmo avere un errore stimabile in 1/10 di
millimetro per ogni tacca e per tanto, nel caso più sfavorevole un
errore di 2/10 di millimetro sulla mezzeria dell'ombra individuata.
Probabilmente questo errore è in effetti di tale entità, a meno di
errata valutazione a vista della mezzeria dell'ombra, però come
vedremo fra poco con esempi pratici, l'errore maggiore non è
relativo alla individuazione di tale mezzeria, ma nella distanza
calcolata dal distanziometro della stazione totale, nella misura in
cui ci si allontana dalla direzione ottimale: strumento–sole,
strumento–oggetto del rilievo, come abbiamo già accennato in
precedenza (vedi Fig.2).10
Come già detto il distanziometro laser integrato nel teodolite ha una precisione (data dal costruttore) di 1 mm, ma in sostanza la misura
ripetuta restituisce misure lineari entro un intervallo di
indeterminazione pari a ±2
millimetri. Ed è proprio questa incertezza che determina l'errore
angolare che a noi più interessa; ed è quello che pesa nel calcolo
della direzione orientata. E l'errore è tanto maggiore quanto più
la stazione di misura tende alla perpendicolare rispetto al tratto
rilevato, tanto da poter dire che per misurazioni veramente precise
sia necessario allineare gli oggetti misurati con la direzione
strumentale. In sostanza dobbiamo fare in modo, per quanto possibile,
di porci nella situazione descritta in Fig. 2, che possiamo definire
“ottimale”, in quanto l'altissima precisione
angolare dello strumento (2 secondi d'arco centesimali11)
supplisce alla meno precisa misurazione lineare, restituendo un
errore sull'orientamento reale, che nel rilievo degli oggetti allineati è teoricamente di soli ±0,010°
(0°0'03.6”) su un tratto di 1,83 m (ombra A1-A2) e di ±0,0004°
(0°0'01,4”) su un tratto di 4,63 m (parete 3-4 da
orientare), dovuta alla indeterminazione di 0.00018° (che equivalgono 2 secondi d'arco centesimali) della lettura al goniometro. Per un errore totale nell'angolo compreso tra A1-A2 e la parete 3-4 pari a ±0.0014° (0°00'05").
Se
invece le misure sono rilevate da posizione non ottimale di una delle
due tratte misurate, o peggio ancora per tutt'e due, prevarrà l'indeterminazione della misura lineare che causerà un
errore che arriva, nel caso da noi rilevato con improvvida scelta
della direzione dell'ombra a ±0,3142°
(0°18'51”) al quale si somma quello della parete pari a ±0,0288°
(0°01'44”), per un errore che può andare da un minimo di 0,2854°
(0°17'07”) ad un massimo di 0,3430° (0°20'35”). Ecco perché è
di fondamentale importanza la scelta della opportuna posizione dello
strumento rispetto al particolare architettonico che genera la ierofania; e medesima importanza ha la posizione dell'asta e dell'ombra da essa proiettata, che devono essere allineate quanto più possibile con la stazione totale e il sole. Per i nostri
studi, in questa scala di valori lineari dell'ordine di pochi
millimetri, poco importa la posizione spaziale più o meno traslata
rispetto alla reale ubicazione dell'oggetto rilevato, ma è di fondamentale
importanza ila precisa misurazione dell'angolo di orientamento.
Per
quanto riguarda l'algoritmo utilizzato dal programma Stellarium,
abbiamo avuto modo di constatare che per la stessa data e ora di
riferimento gli algoritmi del calcolo del ΔT,
deviano dall'azimut del passaggio in meridiano (180°) in un
ventaglio angolare che va da 180°05'28” a 179°59'34”, ossia
0°5'54” di differenza tra il più elevato e il meno elevato su una
scelta di 29 algoritmi, la maggior parte dei quali si attesta
mediamente su 180° ±0°0'5”.
Per tanto optiamo per l'algoritmo di Espenak
& Meeus, formula
predefinita del programma Stellarium12;
tenuto conto oltretutto, che potremmo pure fare a meno del calcolo
del ΔT,
perché stiamo operando all'attualità, e un ritardo di 0°0'5”
d'arco si traduce in una frazione temporale dell'ordine di circa 2/10
di secondo.
L'indeterminazione del programma la rileviamo piuttosto nell'approssimazione a video del tempo, che è pari al minuto secondo; in ragione di ciò l'indeterminazione angolare è pari 0.0047° (0°0'17"), che rapportato al caso reale dell'ombra A1A2 (che vedremo in seguito nel capitolo intitolato "prove e collaudi") come evidenziato in Fig. 3, la distanza di 2.14 m si traduce in una indeterminazione lineare di 0.00017 m, ossia 0.17 mm, che di fatto possiamo assimilare allo spessore di linea di un rapidografo.
Fig. 3
Per
tanto, da questo punto di vista non si rileva alcuna sostanziale indeterminazione da imputare all'algoritmo di calcolo di Stellarium e
in ragione di ciò possiamo affermare con ragionevole sicurezza che
l'errore è relativo alla sola indeterminazione dovuta alla misura
del distanziometro.
In
sostanza stiamo affermando, sulla base della precisione della strumentazione utilizzata e del procedimento applicato (ossia a prescindere da tutti gli errori sistematici e/o casuali), che il metodo adottato sarebbe estremamente preciso, con un
errore che
si
attesterebbe in linea teorica nel caso specifico delle misurazioni effettuate,
attorno a 0°0'05” sessagesimali. Nel prosieguo dello studio vedremo però che l'errore è ben più elevato: dell'ordine dei minuti primi, e questo per una serie di concause che hanno il loro fondamento nella teoria degli errori.
Prove
e collaudi
A
questo punto abbiamo effettuato una serie di prove, utilizzando i
dati di quattro rilievi su altrettante ombre distribuite nell'arco di
alcuni giorni, che hanno restituito i seguenti dati:
Per
ragioni legate alla privacy, saranno indicate in modo approssimativo
le coordinate geografiche dei punti di stazione.
prima
giornata 14/09/2019 ore 16:48:30
stazione 100
coordinate
geografiche 39°55' 3*,**” E 8°41' 2*,**” N
Gli angoli
letti allo strumento sono in gradi centesimali identificati dalla g in apice.
Az. Dist.
punto ombra
A1 0,0000g 5,179
punto ombra
A2 379,1096g 4,161
punto
parete 1 341,8012g 8,205
punto
parete 2 379,0366g 7,816
Si misura
un azimut della parete 1-2 pari a 77,7141°
Fig. 4
seconda
giornata 15/09/2019 ore 15:27:29
stazione
200
coordinate geografiche 39°55' 3*,**”
E 8°41' 2*,**”
N
punto ombra
B1 20,9590g 6,827
punto ombra
B2 29,0862g 7,410
punto
parete 1 0,0000g 8,211
punto
parete 2 37,1918g 7,829
Si misura
un azimut della parete 1-2 pari a 77,5187°.
Fig. 5
terza
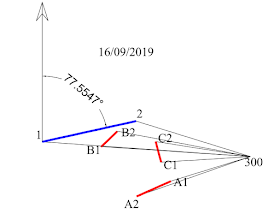
giornata 16/09/2019 ore 12:43:33
stazione
300
coordinate geografiche 39°55' 3*,**”
E 8°41' 2*,**”
N
punto ombra
A2 374,0316g 5,839
punto ombra
A1 376,3800g 4,029
punto ombra
B1 399,7542g 7,272
punto ombra
B2 7,4536g 6,592
punto ombra
C1 391,4416g 4,329
punto ombra
C2 5,5096 g 4,645
punto
parete 1 0,0000g 10,101
punto
parete 2 14,6534g 5,793
Si misura
un azimut della parete 1-2 pari a 77,5547°.
Fig. 6
ancora
terza giornata 16/09/2019 ore 15:20:55
stazione 400
coordinate geografiche 39°55' 3*,**” E 8°41' 2*,**” N
punto ombra
D1 38,0124g 3,290
punto ombra
D2 67,3646g 3,535
punto
parete 1 0,0000g 10,368
punto
parete 2 14,9438 g 6,110
Si misura
un azimut della parete 1-2 pari a 77,5209°.
Fig. 7
Confrontando
i dati notiamo un picco di 77,7141° sulla A1-A2, mentre gli altri
azimut si assestano su valori di 77,5187°, 77,5547°, 77,5209.
Il valore medio tra queste tre misure è di 77,5314°;
con scarti tra la media e quelle estreme di 0,0233° (0°01'24”) e
0,0127° (0°0'46”) e una differenza tra la minima e la massima di appena 0.0360° (0°02'10"). Mentre, tenendo conto della quarta misura
otteniamo una media di 77,5771°; con scarti tra questa e quelle estreme
di 0,0587° (0°03'31”) e 0,1370° (0°08'13”) e una differenza tra la minima e la massima di 0.1954° (0°11'43").
Sulla base di questi azimut rilevati ho confrontato i dati estrapolati dal rilievo per l'accatastamento dell'immobile, di cui fa parte la parete rilevata; dai quali risulta che quella parete è orientata con un angolo di 77,7565° (77°45'23”).
Sulla base di questi azimut rilevati ho confrontato i dati estrapolati dal rilievo per l'accatastamento dell'immobile, di cui fa parte la parete rilevata; dai quali risulta che quella parete è orientata con un angolo di 77,7565° (77°45'23”).
In Google Earth, invece, stimo (in modo approssimativo) un azimut di 77,68° (77°40'48”).
Si tenga conto che il rilievo allegato all'accatastamento dell'immobile è appoggiato a una terna di Punti Fiduciali soggetti a variazione delle coordiante catastali per effetto della rototraslazione effettuata dal programma PREGEO13, per tanto, benché l'orientamento non possa scostarsi in modo significativo dal nord geografico, di certo può variare nell'ordine delle decine di primi d'arco a seconda della terna di Punti Fiduciali utilizzati nel rilievo. Altresì quel rilievo essendo finalizzato all'accatastamento dell'immobile di certo non fu eseguito con altissima precisione visto che per il risultato finale basta l'approssimazione lineare al centimetro ed è tollerato in quell'ambito un errore di 4 cm tra due letture in "andata e ritorno", tra due stazioni tra loro collegate.
Verifica n°2
Una
ulteriore verifica possiamo attuare confrontando la medesima
direzione A1-A2 rilevata il giorno 14 (rilevamento principale) e il
giorno 16 (rilevata per verifica sull'orientamento della C1-C2),
rilevando una differenza di orientamento pari a 0,0331° (0°01'59”);
mentre il medesimo confronto nella direzione della B1-B2 tra il
giorno 15 e il giorno 16 mette in risalto una differenza di
orientamento pari a 0,1849° (0°11'06”). Tenuto conto della
posizione non ottimale delle direzioni rispetto alle stazioni di
rilevamento, possiamo accettare di buon grado gli errori riscontrati,
tenendo conto anche il dato che 2 mm in più e 2 mm in meno in due
misure distinte che descrivono la direzione di un segmento, possono
annullare o raddoppiare l'errore, e ciò giustifica (per certi versi) il grande divario tra
l'errore di 0,0331° (0°01'59”) della prima verifica e 0,1849°
(0°11'06”) della seconda.
Verifica n°3
La quarta
giornata è stata dedicata ad una ulteriore verifica da due diverse
stazioni in allineamento alla parete (denominata più avanti 3-4)
ortogonale a quella già rilevata 1-2. In sostanza ho eseguito un
rilievo utilizzando la direzione A1-A2 dell'ombra del giorno
14/09/2019 e la direzione D1-D2 del giorno 16/09/2019, allo scopo di
quantificare l'errore di misurazione e/o di posizionamento della
direzione dell'ombra.
Stazione 500
coordinate geografiche 39°55' 3*,**”
E 8°41' 2*,**”
N
punto ombra
D1 62,7700g 9,411
punto ombra
D2 62,7822g10,986
punto ombra
A2 67,2784g 4,465
punto ombra
A1 73,0116g 6,226
punto
parete 3 0,0000g 14,911
punto
parete 4 0,0002g 5,757
Stazione 600
coordinate geografiche 39°55' 3*,**”
E 8°41' 2*,**”
N
(la stazione 600 è spostata dalla 500 di 1.35 m verso la direttrice 3-4, per tanto nessuna correzione è necessario
apportare alle coordinate.
punto ombra
D1 71,1084g 8,736
punto ombra
D2 69,8430g 10,298
punto ombra
A2 86,6624g 3,979
punto ombra
A1 86,8006g 5,803
punto
parete 3 0,0000g 13,547
punto
parete 4 0,0694g 4,391
Come
si può evincere dalle misure angolari relative alle stazioni 500 e 600, mi sono premurato di rilevare in linea con lo strumento prima la
coppia di punti D1-D2 e 3-4 dalla stazione 500, che recano per ogni coppia azimut molto vicini, tali da ridurre al minimo l'errore dovuto
all'indeterminazione di ±2
mm nella misura lineare, e in seguito dalla stazione 600, sempre la
coppia di punti 3-4 e la coppia A1-A2. Dalla stazione 500 è stata
anche rilevata la coppia di punti non in linea A1-A2, così la coppia
D1-D2 dalla stazione 600.
Vi
è da dire subito che il valore della indeterminazione dovuto al non
perfetto allineamento dell'asse delle ombre con lo strumento,
generato dalla indeterminazione lineare, è pari a 0,0001° per il
segmento D1-D2 e 0,000014° sul segmento A1-A2.
Il
risultato del calcolo mette in evidenza un errore tra l'azimut della
coppia D1-D2 rilevata dalle due stazioni pari a 0,0517° (0°03'06”)
e un errore della coppia A1-A2 pari a 0,0609° (0°03'39”); mentre
si rileva un errore sulla direzione della parete 3-4 pari a 0,0688°
(0°04'08”).
Fig. 8
Verifica n°4
Naturalmente vi è un certo margine di errore relativo al cambio di stazione (dalla 500 alla 600), per tanto ho effettuato un'altra tornata di misure allo scopo di verificare il margine d'errore, usando la stessa parete, le stesse ombre ma diversa giornata in condizioni meteorologiche diverse, registrando le seguenti misure:
Naturalmente vi è un certo margine di errore relativo al cambio di stazione (dalla 500 alla 600), per tanto ho effettuato un'altra tornata di misure allo scopo di verificare il margine d'errore, usando la stessa parete, le stesse ombre ma diversa giornata in condizioni meteorologiche diverse, registrando le seguenti misure:
Stazione 700
La stazione 700 è vicinissima alla stazione 500, per tanto nessuna correzione sarà apportata alle coordinate geografiche.
La stazione 700 è vicinissima alla stazione 500, per tanto nessuna correzione sarà apportata alle coordinate geografiche.
coordinate geografiche 39°55' 3*,**” E 8°41' 2*,**” N
punto ombra D1 63,2140g 9,393
punto ombra D2 63,1944g 10,970
punto ombra A2 68,0042g 4,445
punto ombra A1 73,6024g 6,208
punto parete 3 0,2102g 14,872
punto parete 4 0,2678g 5,719
Stazione 800
coordinate geografiche 39°55' 3*,**” E 8°41' 2*,**” N
La stazione 800 è vicinissima alla stazione 600, per tanto nessuna correzione sarà apportata alle coordinate geografiche.
punto ombra D1 71,5938g 8,723
punto ombra D2 70,2890g 10,292
punto ombra A2 87,4922g 3,978
punto ombra A1 87,4392g 5,803
punto parete 3 0,2322g 13,506
punto parete 4 0,3872g 4,362
Per tanto possiamo affermare, almeno per ora, che l'errore di indeterminazione è compreso in un intervallo tra 4' e 5' sessagesimali.
Ai fini archeoastronomici è più che sufficiente il grado di precisione rilevato, per il semplice motivo che in molti casi i particolari architettonici che determinano la ierofania luminosa non sempre presentano contorni netti e precisi; tanto che l'errore relativo al particolare architettonico nella pratica è più elevato di 5' minuti primi sessagesimali. A noi però basti sapere che abbiamo la possibilità di calcolare la direzione di un elemento architettonico rispetto al nord geografico con un precisione affetta da un errore di indeterminazione stimato tra 0,0688°
(0°04'08”) e 0.0848° (0°05'05"), che arrotondiamo per difetto a 0°05'00”.
Però l'errore di indeterminazione nella ricerca del nord geografico è insito nel rilievo delle sole ombre ed è pari alla differenza riscontrata nel rilevamento delle medesime da postazioni differenti. E questa differenza è pari a 0.0364° (0°2'11"), nel caso del rilievo effettuato in allineamento (dalle stazioni 500, 600, 700, 800). Se allarghiamo il campo dati e utilizziamo quelli relativi alle stazioni 100 e 400, dalle quali i due tratti A1-A2 e D1-D2 sono stati rilevati in modo indipendente, abbiamo i seguenti angoli compresi:
Tabella "A"
1° 100 A1A2 - 400 D1D2 angolo 21,9205°
2° 300 A1A2 - 400 D1D2 angolo 21,9536°
3° 500 A1A2 - 500 D1D2 angolo 21,8600°
4° 600 A1A2 - 600 D1D2 angolo 21,8692°
5° 700 A1A2 - 700 D1D2 angolo 21,8436°
6° 800 A1A2 - 800 D1D2 angolo 21,8328°
Si tenga presente che è possibile effettuare il raffronto perché le ombre hanno tutte la stessa origine (è il sole che le determina) e la stessa modalità di registrazione.
La media di questi angoli è di 21,8800°, con un divario di 0.0736° con la più alta, e di 0.0472° con la più bassa, e un errore medio di indeterminazione pari a ±0.0604° (0°03'37").
Verifica n°5
Verifica n°5
Vi è però una ulteriore verifica da effettuare, che non è di ausilio, ma è quella che sin dall'inizio avremmo potuto (dovuto) esporre come dato campione.
Abbiamo detto che il rilievo delle ombre è avvenuto il giorno 14/09/2019 alle ore 16:48:30 per la A1A2, mentre la direzione dell'ombra D1D2 è stata registrata il giorno 16/09/2019 alle ore 15:20:55.
In ragione di ciò, il programma Stellarium ci indica che la prima ombra in quel dato momento aveva un azimut di 245.9672°, mentre la seconda ombra aveva un azimut di 224.0465°; la differenza è pari a 21.9207°. Questo ultimo dato, essendo scevro da errori di rilevamento strumentale, ma è affetto solo da errore di indeterminazione del programma Stellarium, ci indica l'azimut campione al quale far riferimento: 21.9207° appunto.
Se tutte le osservazioni strumentali della tabella "A" le riferiamo a questo dato, otteniamo un errore angolare esposto nella sottostante tabella "B" che va da un minimo di:
Tabella "B"
0.0002° per la 1°
-0.0329° per la 2° deviazione di 2.9 mm ad una distanza di 5.00 m
0.0607° per la 3° deviazione di 5.3 mm ad una distanza di 5.00 m
0.0515° per la 4° deviazione di 4.5 mm ad una distanza di 5.00 m
0.0771° per la 5° deviazione di 6.7 mm ad una distanza di 5.00 m
0.0879° per la 6° deviazione di 7.7 mm ad una distanza di 5.00 m
con una media di 0.04075° (0°02'27").In ragione di ciò, a meno di ulteriori rilievi e verifiche, possiamo adottare quale errore medio di indeterminazione che andremo a calcolare, allorquando ci apprestiamo a definire materialmente la direzione del nord geografico, quello (arrottondato) di ±0°02'30"; ossia una precisione piuttosto elevata, che compete con la precisione del GPS usato da Demontis, Contini e Defendente, quale strumento di verifica nelle loro osservazioni. Avendo loro stimato per il GPS un errore pari a 0°02'44".
Volendo anche ammettere, nel nostro metodo, un errore di posizionamento della mezzeria dell'ombra proiettata dalla sommità dell'asta pari a 1 mm, l'errore commesso calcolato sul vertice A1 dell'ombra A1A2, misurata dalla stazione 300 (la più sfavorevole) da una distanza di 4.029 m sarebbe pari a 0.0142° (0°0'51"). Errore che rientrerebbe largamente all'interno dell'errore medio di ±0°02'30".
Conclusioni
Il metodo applicato, naturalmente risente del grado di precisione che l'operatore profonde nella manualità delle operazioni, a partire dal preciso posizionamento verticale dell'asta e preparazione del piano orizzontale che accoglierà l'ombra; della puntualità di intervento sull'ombra da registrare e capacità di discriminare in modo preciso la posizione dell'ombra stessa; nonché nella messa in stazione in maniera corretta e scrupolosa dello strumento di misura (che si ritiene sia stato rettificato), e precisione nel disporre i catarifrangenti sul punto esatto da rilevare. Operazioni che certamente in parte sono frutto di prassi ed esperienza professionale, e in parte frutto dell'esperienza maturata nel campo specifico del rilevamento delle ombre. Tutte operazioni che saranno efficaci e precise se verranno effettuate con la necessaria calma e i tempi giusti.
Il metodo applicato, naturalmente risente del grado di precisione che l'operatore profonde nella manualità delle operazioni, a partire dal preciso posizionamento verticale dell'asta e preparazione del piano orizzontale che accoglierà l'ombra; della puntualità di intervento sull'ombra da registrare e capacità di discriminare in modo preciso la posizione dell'ombra stessa; nonché nella messa in stazione in maniera corretta e scrupolosa dello strumento di misura (che si ritiene sia stato rettificato), e precisione nel disporre i catarifrangenti sul punto esatto da rilevare. Operazioni che certamente in parte sono frutto di prassi ed esperienza professionale, e in parte frutto dell'esperienza maturata nel campo specifico del rilevamento delle ombre. Tutte operazioni che saranno efficaci e precise se verranno effettuate con la necessaria calma e i tempi giusti.
Nei
calcoli di carattere archeoastronomico il valore di
indeterminazione trovato nella misura angolare rispetto al nord geografico, come già affermato, è
ampiamente accettabile in quanto, ad esempio, nel calcolo del
posizionamento del raggio solare all'interno del Pantheon (è il classico caso estremo), nel quale
le ierofanie si manifestano a distanze piuttosto elevate
(dell'ordine di 45 m in misura obliqua da una ipotetica stazione posta in un punto diametralmente opposto all'ingresso che rileva la chiave di volta dell'arco), avremmo un errore di posizione planimetrica pari a poco meno di 3.3 cm14.
Ammesso anche di tener conto dell'errore più elevato: 0.0879° della tabella "B" avremmo, sempre per il Pantheon, un errore lineare di posizione pari a 6,9 cm.
Ammesso anche di tener conto dell'errore più elevato: 0.0879° della tabella "B" avremmo, sempre per il Pantheon, un errore lineare di posizione pari a 6,9 cm.
Negli studi da me condotti sui
pozzi sacri, queste distanze si riducono drasticamente a tutto
vantaggio della precisione profusa.
Abbiamo asserito fin dall'inizio che tutto lo studio è finalizzato alla individuazione dell'orientamento di un edificio rispetto al nord geografico allo scopo di entrare, tramite l'elaborazione di un modello tridimensionale, nell'intima natura della ierofania luminosa che in esso si manifesta.
Per tanto l'errore angolare se pur piccolo, di 0°2'30", è necessario ridurlo a 0°. Infatti una volta realizzato il modello 3D, lo studioso non deve ancora cantar vittoria, ma attendere il momento propizio per effettuare in loco il collaudo di quel modello tridimensionale.Se il modello 3D rispecchia fedelmente, in misure e forme, il monumento reale, è necessario verificare la corrispondenza di luci e ombre in un dato momento prefissato, tra ciò che succede nella realtà dei luoghi, con quello che simula il programma di modellazione. Solo così sarà possibile apportare al modello quelle correzioni angolari (rotazione in solido del modello) che eventualmente dovessero servire per orientare in modo perfetto il monumento al nord geografico. Perché noi possiamo avere lo strumento topografico ultra preciso e usare la massima cura nei gesti del metodo applicato, ma è il sole che comanda e geometricamente giudica.
Alla luce di quanto appena asserito, anche una non precisissima individuazione dei limiti
dell'ombra rilevata, non pregiudicherebbe l'esito del lavoro, ma per
non adagiarsi sugli allori si tenga presente che la precisione tende alla perfezione, per tanto pretende un metodo; e il metodo pretende forma mentis! E
benché la perfezione sia chimerica, la precisione ci aiuta a capire
quel che i nostri avi profusero in sapere e genialità.
Note e riferimenti:
Note e riferimenti:
1 La
migrazione annua del polo nord magnetico è tenuta sotto controllo
dagli scienziati, i quali hanno accertato ultimamente una sua accelerazione.
3 Nell'articolo citato il metodo e la cura dei dettagli furono affrontate in maniera marginale. Questo perché, come gli autori stessi dichiarano, questa procedura è per loro poco più di un esercizio ludico e per tanto esula dal preciso intento di adottare realmente il metodo in campo topografico.
4 L'angolo
di indeterminazione in questo caso dipende anche dalla distanza
della stazione dal tratto rilevato, in quanto più la stazione è
lontana dall'oggetto rilevato più la direttrice OA e OB tendono
alla perpendicolare al tratto AB e di conseguenza aumenta l'errore
angolare, fino ad un massimo, nel caso esemplificato, di 0°0'17 con
la stazione che tende a distanza infinita.
6 Naturalmente
si procederà a posizionare l'asta dopo la messa in stazione dello
strumento topografico in posizione che tende a ovest, in modo
da esser pronti a registrare la posizione dell'ombra quando si
appresta a essere sulla direzione ottimale.
7 La
penombra, come è noto, è dovuta al fatto che il sole non è una
sorgente luminosa puntiforme, in ragione di ciò è possibile
calcolare l'ampiezza della penombra che evidentemente è data dal
diametro apparente del sole che è massimo i primi giorni di gennaio
e al minimo ai primi di luglio. Per tanto il giorno 14/09/2019 il
diametro solare era di 0,52999° e l'ombra vera veniva
assottigliata quel giorno da due angoli convergenti pari alla metà
del diametro solare: 0,264995°.
8 Per
coordinata polare si intende una coppia di dati che definiscono la
posizione di un punto sul piano di riferimento con angolo e
distanza.
9 Fino
all'avvento del CAD nel disegno tecnico, in ambito catastale si
faceva uso del rapidografo, una penna dal tratto preciso e costante, dello
spessore minimo di 1/10 di millimetro. Si potrebbe ancora usate tale
strumento (ammesso sia ancora in commercio, perché ormai fa parte
dei “reperti storici”). Comunque non è un problema reperire uno
strumento capace di tracciare un segno di spessore minimo, perché
si potrebbe optare per altro metodo, ad esempio quello di incidere
con una lametta, o più efficacemente con un cutter o un bisturi e un
nastro adesivo da carrozziere posto sulla tavola orizzontale di
riferimento. Piuttosto ci si deve domandare se sia necessario
profondere tanta precisione.
10 Per
dare una idea dell'errore dovuto allo spessore del segno, sul tratto
di ombra rilevato lungo 1,824 m l'indeterminazione è pari a 0,0063°
(0°0'23” sessagesimali).
11 Si
vuole qui dare una idea di quanto precisa sia la misurazione
angolare di un teodolite moderno. Gli antichi teodoliti meccanici,
per intenderci quelli che furono usati per la formazione della carta
d'Italia, montavano un goniometro sessagesimale che poteva
discriminare con l'aiuto di un nonio i 2” d'arco sessagesimale.
Ossia in un goniometro diviso in 360 parti (gradi), ogni grado era
diviso in 60 parti (minuti primi) e ogni primo in 30 parti (minuti
secondi); per tanto virtualmente tale goniometro era diviso in
360x60x30 = 648.000 parti.
I moderni teodoliti hanno il goniometro
diviso in 400 parti (gradi centesimali), ogni grado è diviso in 100
parti (minuti primi centesimali), ogni primo è diviso in 50 parti
(minuti secondi centesimali); per tanto questo goniometro è diviso
in 400x100x50= 2.000.000 di parti.; ossia più di tre volte più
preciso dei primi teodoliti meccanici.
12 Dalle note esplicative dell'algoritmo, estrapolate dal programma
Stellarium leggiamo: “Questa soluzione di F. Espenak e J.
Meeus, basata sia sul lavoro di Morrison e Stephenson (2004) e un
fit polinomiale su valori tabulati per 1600-2000, è usata per il
sito Web di NASA Eclipse e nel loro Millennium Canon of Solar
Eclipses: -1900 to +3000 (2006). Questa formula è utilizzata anche
nel software per le effemeridi solari, lunari e planetarie SOLEX.
Intervallo di validità: dall'anno -1999 al 3000.”
13 PREGEO
è un programma dell'Agenzia delle Entrate, utilizzato dai
professionisti del settore catastale per l'aggiornamento
cartografico dovuti a tipi di frazionamento e accatastamento di
immobili.
14 A differenza di quanto calcolato ed esposto in Fig.3, per quanto riguarda l'errore di posizionamento nel Pantheon, ma in generale in tutti i monumenti, l'errore essendo strumentale si calcola sulla misura rilevata dallo strumento utilizzato.
14 A differenza di quanto calcolato ed esposto in Fig.3, per quanto riguarda l'errore di posizionamento nel Pantheon, ma in generale in tutti i monumenti, l'errore essendo strumentale si calcola sulla misura rilevata dallo strumento utilizzato.









Nessun commento:
Posta un commento