Il 3 genera il 9. Il 3 e il 9 orientano l'uomo verso la casa del suo dio.

Geometrie e numeri divini

                             Talete di Mileto

di Sandro Angei

vedi 1° parte

Nella prima parte dello studio ci siamo dedicati al problema della divisione in parti congrue di una lunghezza, qualunque essa sia. Abbiamo esposto il metodo, però ahimé non siamo riusciti, almeno per ora (ma non demordo), a dimostrare il teorema. Poi magari la dimostrazione è stata fatta, e sono io, nella mia ignoranza, ad ignorarla. Comunque non è questo il punto e di certo non è l'obiettivo del mio studio la dimostrazione del teorema; dovendo in questo contesto solo giustificare un importante passaggio costruttivo nel pozzo sacro di Santa Cristina.

***

 In questa seconda parte affronteremo una peculiarità emersa nello studio dell'orientamento di quel pozzo sacro e che allora presi come dato concomitante, senza aver ben compreso la cognizione di causa di quella caratteristica.

   In quell'occasione le divisioni del raggio in 3 parti uguali prima e 9 parti uguali dopo, pensavo fossero due dati imposti dal caso "astronomico" e che solo per puro caso fossero uno il quadrato dell'altro. Come invece vedremo tra poco, i due rapporti numerici obbediscono ad una costruzione geometrica che di fatto è un vero e proprio teorema.
    Anche in questo caso, non mi illudo di aver scoperto nulla di nuovo (e sarà cura di chi professa in questo campo a poter dire un “si” o un “no” in tal senso). Fatto sta' che il metodo fu applicato almeno 3000 anni fa dalle genti nuragiche.
   Con questo non voglio affermare che quelle genti usassero in modo cosciente un siffatto teorema di geometria. Semplicemente sfruttarono la proprietà insita in quel teorema perché videro che così facendo riuscivano a orientare il loro sguardo e i loro monumenti in modo estremamente preciso ai solstizi e agli equinozi, lì dove il sole sorge e tramonta a prescindere dalla presenza o meno di rilievi che potessero occultare la vista dell'orizzonte al livello del mare. Una grande conquista, in fin dei conti, visto che l'orizzonte locale poteva spostare verso ovest il sorgere “fasullo” del sole, che spuntava dietro un'altura più o meno vicina all'osservatore.

Il teorema si può enunciare in questi termini:

Fig. 1

Data una circonferenza di raggio R (segmento OA), ed “n” un numero intero positivo; l'arco di circonferenza di raggio R/n con origine “A” che è punto di intersezione di R con la circonferenza, seca detta circonferenza in “C”. La retta mandata dal centro della circonferenza di raggio R al punto “C” seca l'arco di circonferenza di raggio R/n in D, tale che il segmento CD che chiameremo s = R/n²

Per R=1 abbiamo che s = 1/n²

Per tanto:

• per n = 2     AB = 1/2     quindi s = 1/4
• per n = 3     AB = 1/3     quindi s = 1/9
• per n = 4     AB = 1/4     quindi s = 1/16
• per n = 5     AB = 1/5     quindi s = 1/25

e così via.

Dimostrazione

Fig. 2

Il triangolo AOC è inequivocabilmente isoscele con base AC, essendo OA = OC in quanto raggi della stessa circonferenza (Fig.2).

Il triangolo CAD è pure isoscele con base CD, essendo AC = AD in quanto raggi della circonferenza più piccola (ancora Fig.2)

Fig. 3

I triangoli AOC e CAD sono simili perché hanno in comune l'angolo in C (Fig.3).

In ragione di ciò se la base AC del triangolo AOC è 1/3 di OA, la base CD del triangolo CAD è 1/3 del lato AC, di conseguenza il tratto CD è 1/9 del lato OC.

Detto questo, qualsiasi “ennesima” suddivisione operiamo sul raggio R otteniamo un punto secante che dista dalla circonferenza una lunghezza pari al quadrato dell'ennesima parte del raggio.

***

   La proprietà appena enunciata ebbe in età nuragica un interessante risvolto legato all'orientamento astronomico ai solstizi e agli equinozi nel pozzo sacro di Santa Cristina.

In sostanza, probabilmente per mera coincidenza, quelle genti trovarono che una volta individuata la direzione Est-Ovest e di conseguenza la direzione del Nord geografico, costruendo una circonferenza col raggio orientato al Nord geografico, e individuando su di essa, con una sequenza di 3 archi di cerchio pari ad 1/3 del raggio, un punto y sulla circonferenza stessa, si poteva individuata la direzione dell'alba al solstizio d'estate spiccando dal centro O di detta circonferenza il raggio vettore in direzione del punto y (Fig.4).

Fig.4

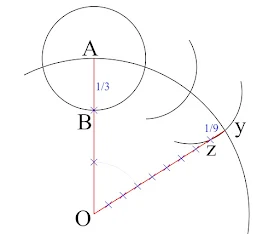
 Inoltre, individuarono il punto della secante che, partendo dal centro della circonferenza arriva al punto y (Fig. 5), intercetta l'arco di cerchio nel punto z tale che la lunghezza yz è pari a 1/9 del raggio.

Fig.5

 Operando una sequenza in "pacchetti" di 5 archi pari a 1/9 del raggio, ottennero la direzione all'alba degli equinozi¹ (Fig.6)

Fig.6

e successivamente con altri 5 archi la direzione precisa all'alba del solstizio d'inverno (Fig.7)

Fig.7

nonché, dopo successivi 5 archi la direzione precisa dell'asse della scala del pozzo sacro (Fig.8).

Fig.8

La verifica

Non paghi di questo risultato, perché sorse in me il dubbio che questa poteva non essere una caratteristica esclusiva della divisione dell'arco in 3 parti, ho eseguito alcune prove relative alla individuazione di dette direzioni fondamentali (alba ai solstizi ed equinozi e della direzione della scalinata del pozzo sacro), suddividendo il raggio in parti numericamente crescenti da 2 a 6 e portando sulla circonferenza un numero di archi necessari alla individuazione dei punti fondamentali richiesti. Il calcolo ha evidenziato quanto riportato nella sottostante tabella A.

Tabella A

N.B.: Per arco primario si intende l'arco di cerchio pari alla divisione imposta pari a 2, 3, 4... parti. Per arco secondario si intende l'arco desunto dalla secante e pari al quadrato della frazione imposta ossia, ad esempio, 1/9 per la divisone imposta di 1/3 di raggio  (Fig.9).

Fig.9

   Leggendo i dati della tabella A su esposta si evince che continuando nella divisione: 7, 8, 9 →∞ per infinite parti, potremmo notare che la direzione del solstizio d'estate si stabilizza sull'angolo di 57°17'45” e il numero degli archi secondari cresce secondo una progressione ben definita pari alla divisione degli archi secondari della divisione precedente più il numero di archi primari di quella in essere, tant'è che in linea teorica la divisione in 7 parti del raggio determinerebbe una quantità di archi secondari pari a 27; la divisione in 8 parti determinerebbe una quantità pari a 35 archi secondari e così via all'infinito ².

   Evidentemente l'angolo di 57°17'45” si ricava per via analitica dalla formula per il calcolo della lunghezza dell'arco di cerchio: l = 2πr x α°/360° dalla quale si ricava per r=1 che α° = l x 360°/ 2πr.

In ragione dei dati esposti nella tabella A, si capisce subito che l'unica divisione efficacemente operabile del raggio R è quella di 3 parti uguali che determina un contenuto numero di archi sia primari: 3, che secondari: 5, e che in definitiva è l'unica che corrisponde in maniera significativa alle caratteristiche riscontrate nel pozzo di Santa Cristina³. Infatti solo questa sequenza di dati è perfettamente compatibile con l'orientamento della scalinata pari a 153°08'.⁴

Conclusioni

Alla fine della trattazione, sperando di essere stati abbastanza chiari nell'esposizione, riteniamo di aver provato che l'orientamento del pozzo di Santa Cristina, ubbidisce a delle regole geometriche ben precise e che quelle genti, con tali regole potevano orientare i loro monumenti ai solstizi e gli equinozi in modo estremamente preciso a prescindere dalla conformazione orografica del territorio che poteva inibire l'osservazione diretta degli eventi astronomici citati.

Considerazioni finali

   Dal punto di vista antropologico possiamo fare la seguente considerazione. Pensiamo per un attimo all'usanza in ambito musulmano di pregare prostrandosi verso la ka'aba  (un edificio a forma di "cubo" che si trova nella Grande Moschea della Mecca). La ka'aba per i musulmani è la casa di Dio. In ragione di ciò i musulmani in qualunque luogo della terra si trovino, verosimilmente nella preghiera orientano il loro sguardo verso la casa di Dio; così come in età nuragica i sacerdoti orientavano in modo più pragmatico e preciso il loro sguardo e i loro edifici in direzione di precise teofanie.

Note e riferimenti bibliografici 

1 Una verifica col programma STELLARIUM evidenzia che alle coordinate del pozzo di Santa Cristina, all'equinozio di primavera il sole sorge al livello del mare ad un azimut di 89°29'06" (differenza rispetto al calcolo geometrico di 0°04'24"). Nel 1000 a.C. sorgeva ad un azimut di 89°37'56" (differenza rispetto al calcolo geometrico di 0°13'14"). Con tutta evidenza differenze così esigue rientrano nell'ambito dell'errore di tracciamento.

2 Vedi infra nota 3.

3 Ciò si intuisce, senza dover effettuare i calcoli necessari, dalla regressione che si riscontra a partire dalla divisione in 4 parti in poi, dove dopo un iniziale incremento sugli archi secondari, si verifica una decrescita costante, per la quale l'incremento di archi secondari non è più in crescita costante ma è necessario un aggiustamento per arrivare agli angoli significativi dei solstizi e degli equinozi.

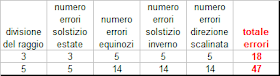
4 Si potrebbe obiettare che comunque anche le altre ipotesi di divisione soddisfano, entro un limitato margine di errore, la condizione richiesta, e ciò è pur vero specialmente per il caso della divisione in 5 parti, per la quale si avrebbe uno scostamento minimo di circa  0°04' per gli equinozi e massimo di circa 0°33' per l'asse della scalinata (vedi tabella A). Però la divisione in 5 parti comporta la suddivisione secondaria in ben 14 parti. In ragione di ciò, dato il carattere pragmatico di quelle genti , carattere che abbiamo tante volte messo in risalto, ben si capisce che comunque sia sarebbe stato poco proficuo se non  del tutto inutile operare una divisione diversa dal 3, non fosse altro che per l'introduzione di un errore di graficismo insito nella ripetuta costruzione di archi. Infatti possiamo dire con tutta sicurezza che l'errore accumulato nella sequenza del 3 (senza entrare nel dettaglio della teoria degli errori e senza contare gli errori grafici di orientamento e divisione del raggio in n parti) è pari in linea teorica a un numero totale di errori (in senso unitario e non in termini di misura) di trasporto di archi pari a:

La tabella mette in evidenza un errore teorico di graficismo pari al 261% della seconda sequenza rispetto alla prima, che legittima ancora una volta l'assunzione della prima sequenza rispetto a tutte le altre.