Il pozzo di Santa Cristina: 2° parte - l'unità di misura
Il pozzo di Santa Cristina: 3° parte - Il sole detta le regole
Il pozzo di Santa Cristina: 3° parte - Il sole detta le regole
8. Il mòdano: una prova tangibile
La funzione del mòdano, come abbiamo
visto soddisfa i requisiti di carattere astronomico e ciò potrebbe
bastare per definire eccezionale quanto scoperto; però non dimostra
fino in fondo che quelle genti conoscessero effettivamente questi
rapporti intercorrenti tra misure lineari e inclinazione dei raggi
solari descritti nel 7° capitolo; ma ancora una volta e in modo sorprendente,
quegli architetti, a testimonianza del loro operato, hanno lasciato
una prova inconfutabile, indipendente dalla meccanica celeste,
perché quel mòdano individuava ad 1/4 della sua altezza
l’inclinazione della scalinata così come doveva essere impostata
originariamente; ossia con una inclinazione di 38°40’.
Proprio questo dato dimostra la conoscenza da parte di quelle genti
di quei rapporti numerici tra geometria e astronomia. Il dato inoltre
è rafforzato dal suo preciso inserimento nella suddivisione in 24 parti del
cateto AB (Fig. 8).
Fig. 8
A questo punto l'ipotesi potrebbe apparire ardua se entrassimo in un ambito piuttosto aleatorio di rapporti numerici che potrebbero esser solo ed esclusivamente frutto del caso, o nella peggiore delle ipotesi, frutto di una insana ricerca (la mia) di un qualche valore che possa verosimilmente coincidere col dato rilevato. Ma sapendo di dover dar conto di un manufatto costruito secondo un ragionamento dettato in gran parte da un modo di pensare pratico, è necessario trovare il sistema che condusse alla scelta di quei rapporti numerici.
Intenzionalità, caso o ricercatore alla ricerca del rapporto numerico?
La
pendenza originaria della scalinata era, come detto, di 38°40', per
tanto le misure di alzata e pedata del gradino sono legate da questa
inclinazione. Osserviamo che i 24 gradini hanno un'alzata media di
24,2 cm, però i primi 7, che possiamo presumere siano quelli della
originale impostazione (vedremo in seguito il perché), hanno
un'alzata media di 24,57 cm. (1,72 m/7 gradini), che impone una
pedata di 30,71 cm. Si noti che la misura di 24,57 cm è in perfetto
rapporto frazionario con la stiba di
43 cm: 4/7
di stiba,
mentre la pedata è nel rapporto di 5/7
di stiba.
Certamente
possiamo trovare numerose frazioni che possano soddisfare, entro certi
limiti, le nostre misure sulla base della stiba;
ma la più vicina coppia di frazioni con medesimo denominatore è 14/25
e 18/25.1
Risulta
evidente che in un range di frazioni compreso tra 1/1 e 20/100 (vedi
nota 1), che conta 2000 diverse combinazioni, non si sta cercando un
qualche rapporto numerico ad
hoc,
ma semplicemente si sta constatando la rarità di questi. In ragione
di ciò è verosimile che i due rapporti 4/7 e 5/7 siano
intenzionali. Meno verosimile è la coppia 15/25 e 18/25 per via di un
denominatore eccessivamente elevato.
L'intenzionalità
comunque non stà nella individuazione su base teorica dei rapporti
di 4/7 e 5/7, piuttosto nella scelta del rapporto ottimale secondo un
procedimento di valutazione del tutto empirico. Procedimento che vede quei due rapporti numerici banale conseguenza e non un dato imposto a priori.
Quale
pensiero possa aver indotto all'assunzione di questi rapporti
numerici ben precisi parrebbe difficile scoprirlo, ma possiamo
pensare che volendo rispettare i rapporti dimensionali con la stiba, quelle genti si siano affidate a questa per impostare la pendenza della scala.
Come possiamo vedere nell'immagine di Fig. 9, la pendenza è imposta dalla misura in orizzontale di 5 stibe (lato AB) e quella verticale di 4 stibe (lato BC).
La dimensione dei gradini fu impostata scegliendo in modo appropriato il giusto rapporto tra alzata e pedata dividendo in un numero preciso di segmenti l'ipotenusa del triangolo rettangolo ABC individuato nel mòdano (vedi ancora Fig. 9).
Come possiamo vedere nell'immagine di Fig. 9, la pendenza è imposta dalla misura in orizzontale di 5 stibe (lato AB) e quella verticale di 4 stibe (lato BC).
La dimensione dei gradini fu impostata scegliendo in modo appropriato il giusto rapporto tra alzata e pedata dividendo in un numero preciso di segmenti l'ipotenusa del triangolo rettangolo ABC individuato nel mòdano (vedi ancora Fig. 9).
Fig.
9
Quei costruttori avrebbero potuto dividere l'ipotenusa AC in qualsivoglia numero di
parti uguali: 5, 6...24. Evidentemente dividendola in 6 parti avrebbero ottenuto frazioni pari rispettivamente a 5/6 e 4/6, se divisa in 12 parti, frazioni di 5/12 e 4/12, e così via. La scelta ricadde sul numero 7; numero che
soddisfa le esigenze “fisiche” del dislivello da superare.
Infatti la divisione in 8 parti avrebbe comportato un'alzata di 21,5 cm e una pedata di 30,7 cm (misure che rientrano in quelle antropometriche ancora oggi usate in alcuni casi); però un'alzata di 21,5 cm x 24 gradini avrebbe superato un dislivello di soli 5,16 m, contro i 5,81 reali.2 Una divisione in 6 parti avrebbe comportato un'alzata di 28,7 cm e una pedata di 45,9 cm. Un'alzata di 28,7 cm x 24 gradini avrebbe superato un dislivello di 6,89 m. Questa suddivisione fu scartata evidentemente, non per l'eccessivo dislivello superabile, piuttosto per le dimensioni non proprio antropometriche dei gradini.3
Infatti la divisione in 8 parti avrebbe comportato un'alzata di 21,5 cm e una pedata di 30,7 cm (misure che rientrano in quelle antropometriche ancora oggi usate in alcuni casi); però un'alzata di 21,5 cm x 24 gradini avrebbe superato un dislivello di soli 5,16 m, contro i 5,81 reali.2 Una divisione in 6 parti avrebbe comportato un'alzata di 28,7 cm e una pedata di 45,9 cm. Un'alzata di 28,7 cm x 24 gradini avrebbe superato un dislivello di 6,89 m. Questa suddivisione fu scartata evidentemente, non per l'eccessivo dislivello superabile, piuttosto per le dimensioni non proprio antropometriche dei gradini.3
Il
giusto rapporto tra dimensione dei gradini e dislivello superabile
con un numero fisso e, oserei dire imprescindibile, di gradini: 24, fu
ottenuto dividendo l'ipotenusa in 7 parti uguali.
***
A prescindere da questi rapporti stringenti tra misure del gradino e la stiba, possiamo dire con tutta sicurezza che nel mòdano sono registrati 6 dati
fondamentali che vennero riportati con i seguenti rapporti numerici:
1, 1/2, 1/3, 1/4, 1/8.
12/24 = 1/2 → 20 aprile - individuazione della base del 12° anello
8/24 = 1/3 → 20 marzo e 23 settembre
6/24 = 1/4 → inclinazione della scalinata
3/24 = 1/8 → 21 dicembre
9.
Numeri e solo numeri
Il
mòdano, così come abbiamo ipotizzato fosse concepito, è di per sé
uno strumento dalle proprietà eccellenti, ma forse nasconde ancora
un particolare non di poco conto.
Naturalmente nessuna prova reale può essere addotta a supporto, per tanto ci accontentiamo delle ipotesi, basate comunque sulla possibile esperienza pratica che quelle genti sicuramente avevano.
Naturalmente nessuna prova reale può essere addotta a supporto, per tanto ci accontentiamo delle ipotesi, basate comunque sulla possibile esperienza pratica che quelle genti sicuramente avevano.
In
questo capitolo prenderemo in considerazione l'ipotesi costruttiva
del mòdano secondo rapporti numerici ben precisi che potenzialmente
quelle genti avrebbero potuto individuare nelle inclinazioni dei
raggi solari rapportati all'unità di misura scelta.
La
curiosità e l'intraprendenza mi ha portato a valutare quale rapporto
numerico in termini di stibe
possa avvicinarsi ai rapporti numerici riscontrati nel mòdano appena
descritto.
Mi
sono imbattuto in un numero frazionario in base 16 (stibe)
rapportabile anche in base 48 (base sulla quale nel 3° capitolo
abbiamo definito la “unità” di 14,33 cm), seconda la quale in un
triangolo rettangolo avente il cateto verticale pari a 16 stibe o 48
unità, l'inclinazione dei raggi solari al
solstizio d'estate è data da una base pari a 5 stibe o 15 unità,
ossia: 5/16 o 15/48 (Fig. 10).
Fig. 10
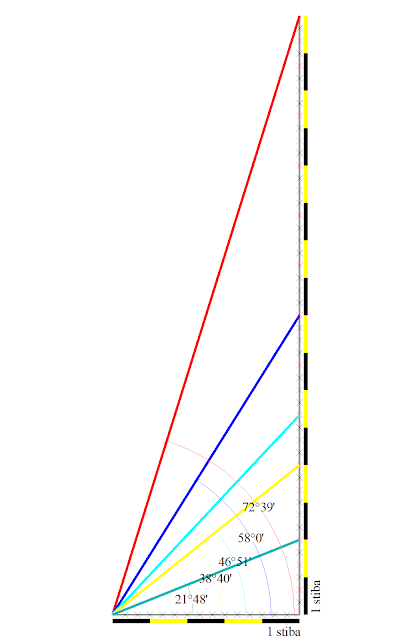
Secondo
questo rapporto numerico otteniamo un mòdano con inclinazione dei
raggi solari al solstizio d'estate pari a 72°39' che è in ottimo
accordo con l'angolo individuato con altro criterio geometrico per
l'azimut di 154°: angolo di 72°27' e con l'altezza astronomica di 72°17'
(vedi tab. di Fig. 4 del 3° capitolo). In ragione di ciò abbiamo
ricostruito il mòdano, che chiameremo “mòdano
rapportato”,
secondo i numeri frazionati su esposti: 5/16, 1/2, 1/3, 1/4 1/8; ottenendo il seguente risultato:
Solstizio
d'estate modano
rapportato
72°39'4
astronomico 72°17' geometrico 72°27'
20
aprile modano
rapportato
58°00'
astronomico 58°49' geometrico 57°41'
20
marzo modano rapportato
46°51' astronomico 46°30' geometrico 46°30'
21
dicembre modano
rapportato
21°48' astronomico 22°34' geometrico 21°34'
scalinata modano
rapportato
38°40' geometrico 38°44'5
Con
tutta evidenza i valori rientrano in tolleranza, tanto da poter
auspicare che la nostra ipotesi possa risultare vera.
Per
tanto il rapporto numerico da memorizzare per la realizzazione dello "strumento" era 5/16, ossia 5 stibe
di base e 16 stibe
d'altezza, per la costruzione della squadra.
Fatto
ciò, per ottenere le inclinazioni dei raggi solari cercate sarebbe stato necessario dividere il cateto maggiore in 24 parti, per individuare
i noti rapporti intermedi di 3/24 (semplificato in 1/8),
6/24 (1/4),
8/24 (1/3)
e 12/24 (1/2).
A ben vedere però non era necessario neanche questa suddivisione
visto che 1/4 è la metà di 1/2 e 1/8 è la metà di 1/4. Per cui la
divisione del cateto maggiore si risolverebbe memorizzando i seguenti
dati:
Il
cateto maggiore lo divido a metà, il tratto inferiore lo divido
ancora a metà, il tratto inferiore lo divido ancora a metà. Segue
la divisione per 1/3 dell'intero (Fig. 11).
Fig.11
Se
ciò fosse vero, come pensiamo sia, il sistema di costruzione del
pozzo di Santa Cristina in particolare, e forse di qualsiasi altro
monumento in generale, sarebbe svincolato completamente da ogni
successiva verifica dell'inclinazione dei raggi solari e si baserebbe
solo sul modulo della stiba
e dei suoi sottomultipli.
Una
considerazione
Le
elaborazioni da me eseguite sono basate su strumenti di alta
precisione, capaci di scandire i secondi d'arco e i millimetri. Col
programma di grafica si possono impostare approssimazioni
estremamente elevate, che comunque sarebbero ridicole in questo
contesto (lo è già l'approssimazione ai secondi d'arco ed il
millimetro); tenuto anche conto che le approssimazioni da me operate sono
estremamente elevate rispetto a quelle che potevano operare 3000 anni
fa con strumenti primitivi; tanto che gli scarti riscontrati tra
mòdano rapportato
e dato astronomico non sarebbe percepibile. In sostanza se eseguissi
materialmente le costruzioni geometriche descritte, con mezzi che
potremmo definire “di fortuna”; per quanta perizia vi possa profondere, di certo le differenze tra dato teorico e dato empirico non
sarebbero rilevabili.
In
ragione di ciò nel prosieguo dello studio possiamo adottare quale
strumento di misura il mòdano
rapportato.
Seconda considerazione
Seconda considerazione
Da quanto fin qui esposto traspare quello che per quelle genti appariva quale "miracoloso messaggio divino". Un messaggio composto di luce, geometrie e numeri. Luce, geometrie e numeri, che prendevano forma attraverso uno strumento materiale: sa stiba, di qualsivoglia misura scelta e che appunto, essendo slegata da qualsiasi unità campione, era unità di misura assoluta che materializzava numeri assoluti. Numeri assoluti che in qualunque luogo e chiunque, benché di diversa estrazione culturale, che fosse Sardo, Egiziano, Babilonese, Indiano, Cinese se non di qualche antica civiltà precolombiana, avrebbe potuto utilizzare. I rapporti numerici di 1/2, 1/3, 1/4, 1/8 sono assoluti, trascendono da qualsiasi unità di misura e per tanto possono essere usati in tutte le unità di misura. Questa fu la geniale intuizione di quelle genti. E se ciò che andiamo asserendo è vero, nei monumenti di età nuragica non dobbiamo cercare unità di misura particolari, ma numeri e solo numeri.
Note e riferimenti bibliografici
1 In un range di 0.5 cm in più o in meno rispetto alle nostre misure i valori sono soddisfati solo dalle frazioni 15/25 e 18/25 in un gruppo di frazioni da 1 a 20 al numeratore e 1 a 100 al denominatore. In questo range di frazioni, che conta 2000 diverse combinazioni, 15/25 e 18/25 sono le uniche frazioni ,dopo 4/7 e 5/7, che soddisfano l'univocità del denominatore e per approssimazione, il dato metrico.
2 5,81 m è il dislivello che misuriamo attualmente nella scalinata, che però, a quanto pare, fu oggetto di ricostruzione da parte dell'archeologo E. Atzeni. Sembra verosimile, secondo le misure ipotetiche da me individuate, che il dislivello originario fosse di 28,57 cm x 24 gradini = 589,68 cm (colgo l'occasione per dire che la seconda cifra decimale è puramente estetica, essendo dell'ordine del decimo di millimetro; tant'è che se avessi espresso le misure in metri avrei scritto 5.90 m e non 5.8968).
3 Si noti che nella progettazione di una scala si tende a dimensionare i gradini nella proporzione ottimale di 17 cm di alzata x 30 cm di pedata. In alcuni casi, come nelle scale a chiocciola, si tende ad elevare l'alzata fino a 21 cm e anche più.
5 L'inclinazione
è stata misurata dal bordo del 2° gradino al bordo del 7°
gradino.





Un amico, benché sia affezionato lettore dei miei studi, mi ha confidato di avere difficoltà a districarsi tra tutti i numeri esibiti in questo articolo.
RispondiEliminaSin dall'inizio ero cosciente del difficile approccio a questo studio. E' un articolo molto tecnico certamente, ma penso dia spazio a riflessioni in vari ambiti di studio. Prendendo in considerazione solo l'aspetto numerico, invito il lettore a concentrarsi sull'aspetto filosofico dei numeri; al di là di quelli che possono essere i freddi numeri, che siano essi relativi a misurazioni angolari o misurazioni di una lunghezza oppure entità pura del numero manifestata da una frazione. Nel dell'articolo si troveranno spunti di riflessione per dare risposta ad una domanda che in ambito della “filosofia della matematica” chiede “perché e in che modo gli enunciati matematici sono veri.” Qui non si pretende di arrivare a tanto, però nel ristretto tema qui trattato, si capirà alla fine dello studio perché alcuni numeri, in ambito nuragico, sono assurti a valenza sacrale.
Caro Sandro, forse ha ragione il tuo affezionato lettore, ma a me fa meraviglia non tanto i ragionamenti complicati che esponi, quanto la determinazione con cui ti sei mosso per cercare le relazioni e le motivazioni che supponevi dovessero essere alla base di una costruzione che ancora oggi sa di stupefacente.
RispondiEliminaSarebbe oltremodo stupido pensare oggi che le ierofanie si presentino per puro caso, quando hai dimostrato che tutto, ma proprio tutto, segue un progetto razionale per quantità e dimensionamento degli elementi costitutivi, per l'orientamento degli stessi e per la congruità fra di loro.
Mi viene da darti un consiglio sottovoce: sarà meglio che ti fermi, sennò si divulgherà l'idea che a costruirla così perfettamente non siano stati gli antichi Sardi, presunti nostri antenati nonché pastori litigiosi, ma qualche prode architetto venuto dall'Oriente come i Re Magi, o un qualche alieno, come dicesi della grande Piramide.
Stai cauto! Coi numeri e con l'immaginazione.
Caro Francu, non sai quante volte mi son domandato se quello da me scoperto sia frutto della mia fantasia o davvero il frutto della genialità di quelle antiche genti.
RispondiEliminaHo dato una risposta a questa domanda, che forse soddisferà solo me, ma che comunque esposta con le necessarie motivazioni potrà essere giudicata, più o meno scientemente, dal nostro lettore.
Come avrai avuto modo di capire - spero che tutti lo abbiano capito – parte dei numeri esposti sono dettati dal moto astronomico del sole, non certo dal volere di quelle genti, che nello specifico hanno solo osservato e appreso; come io stesso ho osservato e appreso. Tutti gli altri numeri e rapporti numerici non dobbiamo interpretarli nella loro forma matematica: 1/3, 2/3, 3/4 e via dicendo, me nella loro veste più materiale di parti di un tutto, scandendo le quantità in termini di 1 di 3, 2 di 3 e così via.; la qual cosa sembrerà banale, ma è più ragionevolmente semplice.
Tutto il resto (ma ancora siamo a metà dell'opera) implica osservazione e manualità nei gesti; nulla di più.
Caro Sandro, io mi sono già trovato a scrivere che con i tuoi studi sembri fondare da solo una disciplina; un giudizio magari eccessivo e che, detto da me, varrà nulla. Anche questa volta, però, mi sembri riuscire da pioniere in obiettivi che non avevano ancora sfiorato che pochissimi, e che nessuno prima (per il poco che so) avrebbe mai avvicinato a tal punto. Per questo ti rinnovo tutta la mia ammirazione.
RispondiEliminaÈ naturale che i commenti latitino, qui non è facile entrare nel merito a osservare qualcosa oltre il tanto che osservi da solo. E non sono contenuti da accompagnare con una claque.
Credo, nonostante la pesantezza, tu faccia bene a fondare lo studio con questi articoli ponderosi, dove ci spieghi passo passo non solo come loro fossero arrivati a tanto, ma anche come tu sei arrivato a ritrovarne i passi. Spero (vorrei dire: confido) che alla fine produrrai, come ultimo sforzo, un riassunto più semplice, che sulla scorta di tante necessarie premesse potrà risultare meglio fruibile dai più (e che permetterà ai volenterosi di ripercorrere lo studio riuscendo a seguirlo meglio).
Naturalmente si spera giunga soprattutto l’attenzione dei ricercatori, di cui ti chiederei (forse ancora prematuramente) se hai già avuto qualche sentore.
Amico mio, il Prof. Sanna ti ha definito “storiografo” della scrittura nuragica, e ben ci stà, visto l'impegno profuso in tanti anni che hai dedicato con assiduità al tema, in seguito sfociato in un bel libro. Non ti chiedo di fare altrettanto con me; però lamentando una “pesantezza” di questo studio (direi anche “mattone”, visto lo snocciolamento di dati), da buon storiografo hai colto nel segno. Questo studio è indirizzato ai seri ricercatori e a tutti quei volenterosi che vogliano andare un po' oltre la lettura automatica. Non faccio questo per me naturalmente, non sono così sfacciato; lo faccio per quelle antiche genti, che è giusto abbiano, se è vero ciò che affermo, il dovuto riconoscimento di uomini “civili”... molto civili!
RispondiEliminaFrancesco, come tu ben dici “non sono contenuti da accompagnare con una claque” quelli qui esposti, e non sarò io a chiedere applausi; penso comunque che la latitanza dei commenti in questo blog, e non solo in questo blog, non sia dovuta alla difficoltà del tema, quanto a una qualche “paura” di quei lettori competenti. Lettori che ci sono e anche numerosi direi.
Perché non commentano? Perché siamo nella stessa situazione della questione “scrittura nuragica”.
Vien detto che la scrittura nasce in ambito palaziale, in seno alla città, per via del commercio etc. etc.
Il sapere di geometria, matematica, astronomia, topografia, architettura etc. etc., è certamente segnale di un alto grado di civilizzazione, quella stessa civilizzazione che per l'Accademia basa il suo “essere civile” sulla scrittura. Il paradigma è chiaro quanto semplice. Lo stesso paradigma (lo scrissi in un commento su facebook e apro una parentesi) adottato dal Dr. A. Usai quando in una conferenza in Cabras agli inizi di gennaio di quest'anno, espresse il suo pensiero a riguardo di due domande poste dal pubblico a riguardo (la prima) della strada che da Tharros passa per la necropoli di Monte prama, per raggiungere forse le miniere del Montiferru? La seconda in relazione ai segni di ruote di carro trovate lungo la strada. La risposta fu che “Quando era fiorente Monti prama, Tharros era ancora li da venire” (tra le righe dobbiamo leggere: Visto che i fenici non erano ancora arrivati e per tanto non vi era alcuna strada tra Tharros e Monte prama?). Per quanto riguarda i solchi, invece, l'Accademia ritiene che siano dovute a slitte (alcuni hanno sorriso pensando a slitte da neve) altri come me hanno subito pensato a slitte tipo quelle degli indiani d'America. Tra le righe anche qui dobbiamo leggere: “Visto che i fenici non sono ancora arrivati, quei segni non sono dovuti ad alcuna ruota, ma a ben più rudimentali mezzi trascinati”?
Chiusa la parentesi; ecco che risulta imbarazzante, escludere l'esistenza della scrittura nuragica e contemporaneamente ammettere che i nuragici oltre ad essere provetti architetti conoscitori dell'arco a conci prima e della ben più sofisticata “falsa cupola” (sic!) dopo; e oltre a intendersi di idraulica (Gremanu) Su Tempiesu) si intendevano di idraulica sofisticata come a Santa Cristina col suo impianto di troppopieno sifonato; di architettura luminosa (come dimostro ormai da qualche tempo e non solo io); geometria e non quella spicciola del semplice cerchio (il fallo di Gremanu e il recinto di sacro di Santa Cristina per dirne alcuni); astronomia, e anche qui non quella spicciola data da tre elementi: osservatore, punto fisso all'orizzonte, stella o sole che sorge o tramonta e per tanto in situazione di minimo impatto luminoso sull'occhio umano. Qui si parla d'altro; e le sorprese, caro Francesco, non sono ancora finite.
Io spero che tutte le cose che stai scrivendo vengano raccolte in un libro che farebbe buum! specialmente se edito anche in inglese. Pensaci, se ancora non l'hai fatto.
RispondiEliminaNon sei il primo a chiedermi di fare questo. Per il momento finiamo di pubblicare tutto lo studio, poi si vedrà.
EliminaThank you for thiss
RispondiEliminaThank you
EliminaQuindi, se ho capito bene, l'inclinazione della scalinata permette al sole di raggiungere l'acqua non durante tutto l'anno. Il solstizio d'inverso ad esempio è sotto l'angolo della scalinata (fig 11)
RispondiEliminaMa neanche al solstizio d'estate perché i raggi solari hanno una inclinazione troppo elevata.
Elimina