Ancora sul problema dell'orientamento degli spigoli al vertice della Grande Piramide
di Sandro Angei
7. L'altezza della piramide scienza o caso?
Abbiamo detto alla fine del 5° capitolo della 3° parte che le considerazioni di carattere geometrico e matematico lì esposte sono frutto di esperienza personale proiettata in quel cantiere di 4500 anni fa, ma con le cognizioni "del senno di poi".
Per tanto in questo capitolo affronteremo un nuovo quesito. E' necessario, cioè, capire se l'inclinazione del dispositivo, da noi chiamato "mòdano", fu frutto di un rapporto numerico prediletto per pura simbologia, e di conseguenza fu casuale anche l'altezza della piramide, oppure se fu calcolata analiticamente sia l'una che l'altra, e in tal caso, come fecero a effettuare il calcolo?
I dati in nostro possesso ci inducono a pensare alla probabilità che quegli architetti avessero stabilito a priori le misure della piramide:
lati di base e altezza. Se ciò non fu, il problema non si porrebbe... ma noi non possiamo non tenerne conto, data anche la prova concreta che quegli architetti avevano un sufficiente grado di conoscenza sia della matematica che della geometria (papiro di Ahmes).E' necessario in definitiva dimostrare che quegli architetti riuscivano a pensare in astratto, ossia realizzare un disegno in scala dell'edificio.
Erano in grado di fare questo? (12) La domanda sembrerebbe porre qualche dubbio di fattibilità, ma di fatto la Grande Piramide è sotto i nostri occhi; è essa stessa la prova che quelle genti erano in grado di progettare. Ma noi non possiamo dare per scontata la risposta, né tanto meno accoglierla ad occhi chiusi, sicuri della prova autoreferente. Dobbiamo cercare il metodo, se pur ipotetico, che condusse quegli architetti a realizzare questa magnifica costruzione.
Per tanto rispondo alla domanda nel seguente e banalissimo modo: se la risposta è affermativa il metodo qui ipotizzato per indirizzare gli spigoli della costruzione fu dettato da cognizione di causa, altrimenti fu adottato quale metodo empirico, senza però saper governare a piacimento la misura in altezza della piramide.
Comunque sia, se l'altezza della piramide fosse dovuta a mero caso, non di meno è risolutivo il metodo di indirizzamento degli spigoli al vertice, descritto nella parte 3° dello studio, perché bastava realizzare quattro mòdani uguali, da orientare tutti nel verso delle diagonali e distanza identica per tutti dal relativo spigolo di base (13). Ma noi siamo dell'idea che l'altezza fu determinata a ragion veduta e per tanto ora ci accingiamo ad ipotizzare un metodo logico-deduttivo.
7.1 Analizziamo i dati in nostro possesso
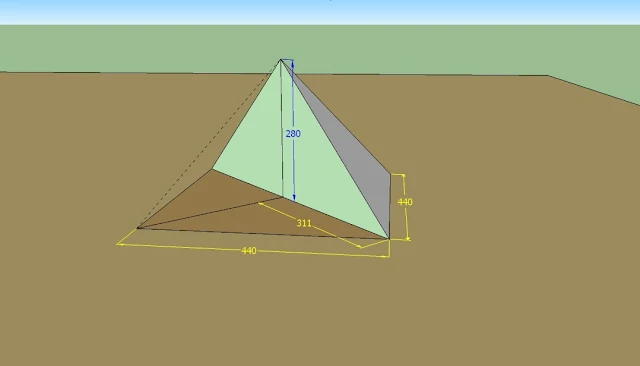
Il lato di base della piramide è di 440 cubiti reali equivalenti a 230,384 m; l'altezza originale della piramide era di 280 cubiti equivalenti a 146,608 m (Fig.26) (14); per tanto le semi diagonali di base dovevano avere una lunghezza di 162,906 m equivalenti, approssimativamente, a 311 cubiti che equivalgono precisamente a 162,840 m, ossia una differenza rispetto al dato teorico di soli 6,6 centimetri.
Facciamo la prova.
7.2 A scuola di disegno e geometria
Innanzi tutto è necessario introdurre il concetto di scala di rappresentazione ossia, un segmento di una data lunghezza equivale ad un segmento, poniamo, due volte più lungo. In ragione di ciò costruendo due triangoli rettangoli: il primo di due Cr di base e un Cr di altezza, il secondo di due mezzi Cr di base e un mezzo Cr di altezza otteniamo di fatto due triangoli simili che hanno le ipotenuse parallele, ed è facile dimostrarlo empiricamente facendo coincidere il vertice E col vertice B oppure il vertice F col vertice C dei due triangoli (Fig.27).
Evidentemente il passo successivo è quello di ridurre la dimensione del segmento usato come rappresentazione virtuale della realtà secondo un sottomultiplo del cubito reale; per tanto potremmo sostituire il nostro Cr col palmo o addirittura col dito (15) e usarli, l'uno o l'altro, quale rappresentazione virtuale del cubito vero e notare che pure in questo caso la sovrapposizione del triangolo (ILM) che abbiamo costruito con 2 palmi di base e 1 palmo di altezza ancora mantiene la stessa inclinazione del lato obliquo (Fig.28).
7.3 Due triangoli, stessa altezza diversa base
Il passo successivo impone la risoluzione del problema relativo al calcolo dell'altezza del triangolo IGH di Fig.28, partendo da un triangolo con la base maggiore di quello dato e che chiameremo "triangolo mòdano" (da non confondere col "mòdano" che designa lo strumento di controllo).
Perché sia necessario risolvere questo problema lo si intuisce dal problema pratico che gli antichi Egizi dovettero affrontare nella realtà del loro cantiere e che abbiamo spiegato in modo tecnico nel quinto capitolo (3° parte del saggio).
Per tanto mi immedesimo nell'architetto egizio e facendo ancora riferimento al triangolo rettangolo ILM di Fig.28, voglio impostare la sua altezza secondo un punto esterno al triangolo stesso. Per fare ciò, ed essere sicuro di risolvere il mio problema, costruisco un triangolo rettangolo (Fig.29) partendo dal vertice I di altezza pari a "un palmo" (IL) e la base lunga "3 palmi" (LN). Se prolungo il lato inclinato IN di questo triangolo, questo incontrerà il prolungamento della base GH in O, notando che l'allungamento della base è pari a "7 palmi"; e se misuro la base del triangolo IGO conto "21 palmi"; per tanto questo triangolo è 7 volte più grande del triangolo ILN. Di fatto col triangolo IGO di Fig.29 abbiamo realizzato quello che poco sopra abbiamo definito "triangolo mòdano" che è in rapporto ben preciso col triangolo IGH: stessa altezza diversa base. Per tanto d'ora in poi parleremo di "triangolo mòdano" (IGO) e di "triangolo di progetto" (IGH, quello che in definitiva rappresenta, naturalmente con misure diverse, la semi sezione della piramide)
7.4 Dalla teoria alla pratica
Andiamo oltre e prediamo in considerazione la Grande Piramide e usiamo per progettarla proprio il metodo appena descritto, ma partendo dall'inizio con la nostra progettazione pensando ancora come l'architetto egizio. Almeno così, spero!
Ricordiamo che il sistema di misure lineari dell'antico Egitto prevede il Cr diviso in 7 palmi, ogni palmo diviso in 4 dita, ciò significa che un Cr equivale a 28 dita.
Per tanto potendo impostare le misure di "mia iniziativa" assegno al lato di base della grande piramide la misura di "440 Cr" e alla sua altezza la misura di 280 Cr. Così almeno semplifico il calcolo. (16)
Dovendo realizzare il progetto "in scala" mi basta pensare che un dito possa equivalere ad un Cr, per tanto traccio a terra una linea di 440 dita (8.228 m), che naturalmente misuro con 15 Cr + 5 palmi (altrimenti a cosa servirebbero i sottomultipli?!); dopo di che traccio una perpendicolare alla prima, lunga altri 15 Cr + 5 palmi. Traccio la diagonale sulla quale misuro 22 Cr + 1 palmo + 2 dita (11.634 m), ottenendo una soddisfacente approssimazione, perché traducendo tutto in dita ottengo 622 dita (col resto di 4.7 mm, circa 1/4 di dito).
Ottenuta la misura precisa della diagonale la divido per due ottenendo la misura di 311 dita, ossia 11 Cr + 3 dita (5.82 m) e la riporto sempre a terra. Traccio una linea perpendicolare a questa e misuro 280 dita (che equivalgono a 10 Cr).
Per tanto, ho ottenuto un triangolo rettangolo con la base di 311 dita e l'altezza di 280 dita che simula la semisezione verticale della piramide in corrispondenza della diagonale (vedi ancora Fig.26).
Proviamo in modo empirico a verificare quale possa essere il rapporto ottimale tra l'altezza di "280 dita" e la base del "triangolo mòdano" (triangolo IGO dell'esempio teorico di Fig.29), che vada oltre la semi diagonale di progetto della piramide (quello che abbiamo chiamato "triangolo di progetto" - triangolo IGH), e questo perché il nostro rapporto numerico deve basarsi proprio sul numero 280; per tanto la base del "triangolo mòdano" deve essere un numero moltiplicabile o divisibile senza resto per 28 (lo abbiamo visto nella tabella B allegata alla 3° parte dello studio). Il rapporto ottimale, trovato è quello di "4 dita" di altezza e "5 dita" di base: 4/5 (28 è divisibile per 4). Pertanto, usando questo rapporto, otteniamo un "triangolo mòdano" di "280 dita" di altezza e "350 dita" di base, (perché 280 è 4/5 di 350). In ragione di ciò possiamo dire che dobbiamo prolungare la diagonale di base della nostra piramide in scala di "39 dita" oltre le "311 dita" già segnate della semi diagonale (che di fatto è la base del "triangolo di progetto". Riportando le misure in cantiere dovremmo prolungare nella realtà la diagonale di base della piramide di 39 Cr.
Non rimane che calcolare le misure reali del "mòdano" (il nostro strumento di controllo) che ci servirà in cantiere; per tanto avendo stabilito che il rapporto ottimale sia quello di 4 dita di altezza e 5 dita di base, non rimane che tradurre tutto in Cr.
7.5 Andiamo in cantiere
Tutto si gioca su quei 39 Cr esterni alla base e quel rapporto numerico di 4 Cr di altezza e 5 Cr di base (Fig.30 e 31).

Fig.31 - vista d'insieme
Partendo dall'estremo di quel tratto di 39 cubiti (vertice Q di Fig.30), poniamo sul prolungamento della diagonale un picchetto a 5 Cr di distanza (in alternativa a 10 Cr se ci sembra che il modano sia troppo piccolo), e da lì innalziamo un palo o una impalcatura che dovrà raggiungere l'altezza di 4 Cr (in alternativa 8 Cr) sulla verticale di quel picchetto.
Il più è fatto: basta tendere una funicella dal vertice estremo posto a 39 Cr dalla base al punto posto a 4 Cr di altezza per ottenere la direzione esatta da tenere nella costruzione dello spigolo della piramide.
Il lavoro di ingegno è terminato, si dia inizio ai lavori!
Per tanto è verosimile che quegli architetti abbiano utilizzato un mòdano triangolare di queste proporzioni per i loro controlli di cantiere.
Con queste specifiche tecniche installiamo il nostro congegno, ottenendo così un dispositivo capace di tenere sotto controllo sia la direzione azimutale della semi diagonale sulla qui verticale si innalza lo spigolo verso il piramidion (Fig.32), sia l'inclinazione dei due spigoli inclinati costruiti sulla diagonale ortogonale alla prima. E questo senza dover installare alcun marchingegno sulla piramide in costruzione, perché di fatto l'ipotenusa del triangolo rettangolo del nostro mòdano punta verso il vertice; per tanto all'operatore che traguarda, basta trovare il punto esatto dal quale vede coincidere l'angolo di base della piramide posto di fronte a lui (abbiamo descritto la sequenza nella 3° parte) con la lenza inclinata che punta verso il vertice, benché quest'ultimo sia ancora virtuale.
Se installiamo questo congegno in modo stabile su ogni angolo della piramide (congegno che non intralcia in alcun modo l'iter lavorativo), possiamo tenere simultaneamente sotto controllo ogni spigolo della grande piramide da tre congegni diversi (Fig.32).








Stupendo Sandro! E stupisci sempre di più.
RispondiEliminaCaro Professore, consapevole che il suo giudizio non è per nulla gratuito, visti i vincoli che impone dal punto di vista filologico, con consapevole piacere accolgo questo suo commento, e mi sento di dire il perché questi studi possano stupire.
RispondiEliminaL'impostazione di questi studi non può prescindere dalla necessaria condotta interdisciplinare. L'archeologo arrivato ad un certo punto, non può andare oltre con i soli suoi studi; è necessario l'ausilio di altre discipline che, nella loro scientificità, possano supportare con prove evidenti o anche solo con ipotesi, però verosimili e circostanziate, il risultato al quale, il più delle volte, la sola archeologia può constatare il solo dato di fatto, o avanza ipotetiche funzioni basate solo su ciò che lo studioso lì impegnato conosce, eludendo di fatto tutto ciò che "non" conosce.
Succede qui in Sardegna, dove non si è capita la funzione della porta del sole di Murru mannu in Tharros; oppure la vera funzione del pozzo di Santa Cristina e di altri ad esso simili e quella del pozzo di Is pirois; e succede in Egitto dove del modo di costruire delle grandi piramidi si è dibattuto, più o meno a tentoni da secoli – ormai! - e questo perché si sono saltati a piè pari tanti passaggi “costruttivi”, il più importante dei quali è proprio quello trattato in questo saggio.
Arrivati a questo punto degli studi, non rimane che affrontare con nuovo spirito e la scorta della tecnica costruttiva di controllo appena trattata, il metodo di edificazione della grande piramide, non tralasciando alcun particolare come, ad esempio, lo spazio necessario alla manovra di conci isodomi di data misura in ambiente angusto, oppure la modalità di ventilazione in galleria e la specifica operazione di rivestimento delle facce oblique, la finitura e lisciatura di queste e le modalità di discesa dal vertice della piramide una volta posizionato il piramidion. E tutto questo senza dover ricorrere a rampe esterne.
Solo alla fine dell'opera, quando si arrivò in alta quota, probabilmente si dovette ricorrere per evidenti esigenze di cantiere, ad una modesta impalcatura esterna.
Non ho idea di quali idee tu abbia piena la testa; la mia idea è che tu quelle idee le abbia chiare in testa.
RispondiEliminaCaro Francu, è indispensabile e vitale avere le idee chiare, altrimenti "i minestroni" son lì, dietro l'angolo. A quanti "minestroni" abbiano assistito specie in Facebook?! Quanti "finestroni", capaci di inquadrare intere costellazioni, qualcuno evocò qualche tempo fà su questo blog. Quanti "maestroni" cercano di propinarci improbabili civiltà "sardo-atlantidee" senza uno straccio di prova, senza studio, né ricerca, ma all'insegna della fede incondizionata che gli audenti debbano avere in loro. Io non ci sto a questo modo di fare, ragionare e dire... io seguo la rigidità matematica e geometrica, quella che poi sposa benissimo la filologia, quella usata in modo incondizionato da Gigi Sanna.
EliminaCerto che per seguirmi per alcuni e dura fatica, almeno quanto la mia che vi ho ragionato sopra; ma questo è il prezzo da pagare se si vuole sapere.
E tutto ciò ha bisogno di lucidità mentale.
Caro Sandro, è la solita questione che si pone nella vita di tutti: essere o avere? Essere o apparire?
RispondiEliminaEcco, c'è chi sceglie di essere quello che vorrebbe essere nella vita, anche a costo di rinunce, fatica e sacrifici; c'è invece chi se ne frega e si ritaglia un vestito piacevole per apparire in pubblico oppure sceglie ogni giorno il proprio tornaconto, costi quello che costi, a lui stesso e agli altri.
Ti pare che ho detto bene?
Spero che abbia fatto di no con la testa: sono solo cavolate!
Però tu mi hai fatto la predica, ma non mi hai detto neppure grazie, perché il mio era un complimento. Singolare, strano, tutto quello che vuoi, ma pur sempre un complimento.
E le tue lezioni matematiche di un "quadrato elevato a piramide" non mi danno gioia, non mi consolano, non mi fanno guadagnare niente. Eppure le ho lette (e le ho pure capite, ndr), solo perché mi piace saperle.
Certo che ho capito il tuo complimento e te ne rendo grazie. La predica non era rivolta a te, che non né hai bisogno, ma ad altri, che fanno di tutte le idee un fascio.
Elimina