di Sandro Angei
8. Il mòdano: una prova tangibile
La funzione del mòdano, come abbiamo
visto soddisfa i requisiti di carattere astronomico e ciò potrebbe
bastare per definire eccezionale quanto scoperto; però non dimostra
fino in fondo che quelle genti conoscessero effettivamente questi
rapporti intercorrenti tra misure lineari e inclinazione dei raggi
solari descritti nel 7° capitolo; ma ancora una volta e in modo sorprendente,
quegli architetti, a testimonianza del loro operato, hanno lasciato
una prova inconfutabile, indipendente dalla meccanica celeste,
perché quel mòdano individuava ad 1/4 della sua altezza
l’inclinazione della scalinata così come doveva essere impostata
originariamente; ossia con una inclinazione di 38°40’.
Proprio questo dato dimostra la conoscenza da parte di quelle genti
di quei rapporti numerici tra geometria e astronomia. Il dato inoltre
è rafforzato dal suo preciso inserimento nella suddivisione in 24 parti del
cateto AB (Fig. 8).
Fig. 8
Quelle genti avrebbero potuto scegliere una inclinazione della scala più agevole, ma in in un progetto nel quale la stiba è utilizzata quale unità di misura di riferimento, anche il
gradino doveva rispettare dei rapporti ben precisi; rapporti che abbiamo scoperto essere 4/7 e 5/7 di stiba.
A questo punto l'ipotesi potrebbe apparire ardua se entrassimo in un ambito piuttosto
aleatorio di rapporti numerici che potrebbero esser solo ed
esclusivamente frutto del caso, o nella peggiore delle ipotesi, frutto di una insana ricerca (la mia) di un qualche valore che possa verosimilmente coincidere col dato rilevato. Ma sapendo di dover dar conto di un manufatto costruito secondo un ragionamento dettato in gran parte da un modo di pensare pratico, è necessario trovare il sistema che condusse alla scelta di quei rapporti numerici.
Intenzionalità, caso o ricercatore alla ricerca del rapporto numerico?
La
pendenza originaria della scalinata era, come detto, di 38°40', per
tanto le misure di alzata e pedata del gradino sono legate da questa
inclinazione. Osserviamo che i 24 gradini hanno un'alzata media di
24,2 cm, però i primi 7, che possiamo presumere siano quelli della
originale impostazione (vedremo in seguito il perché), hanno
un'alzata media di 24,57 cm. (1,72 m/7 gradini), che impone una
pedata di 30,71 cm. Si noti che la misura di 24,57 cm è in perfetto
rapporto frazionario con la stiba di
43 cm: 4/7
di stiba,
mentre la pedata è nel rapporto di 5/7
di stiba.
Certamente
possiamo trovare numerose frazioni che possano soddisfare, entro certi
limiti, le nostre misure sulla base della stiba;
ma la più vicina coppia di frazioni con medesimo denominatore è 14/25
e 18/25.
Risulta
evidente che in un range di frazioni compreso tra 1/1 e 20/100 (vedi
nota 1), che conta 2000 diverse combinazioni, non si sta cercando un
qualche rapporto numerico ad
hoc,
ma semplicemente si sta constatando la rarità di questi. In ragione
di ciò è verosimile che i due rapporti 4/7 e 5/7 siano
intenzionali. Meno verosimile è la coppia 15/25 e 18/25 per via di un
denominatore eccessivamente elevato.
L'intenzionalità
comunque non stà nella individuazione su base teorica dei rapporti
di 4/7 e 5/7, piuttosto nella scelta del rapporto ottimale secondo un
procedimento di valutazione del tutto empirico. Procedimento che vede quei due rapporti numerici banale conseguenza e non un dato imposto a priori.
Quale
pensiero possa aver indotto all'assunzione di questi rapporti
numerici ben precisi parrebbe difficile scoprirlo, ma possiamo
pensare che volendo rispettare i rapporti dimensionali con la stiba, quelle genti si siano affidate a questa per impostare la pendenza della scala.
Come possiamo vedere nell'immagine di Fig. 9, la pendenza è imposta dalla misura in orizzontale di 5 stibe (lato AB) e quella verticale di 4 stibe (lato BC).
La
dimensione dei gradini fu impostata scegliendo in modo appropriato il
giusto rapporto tra alzata e pedata dividendo in un numero preciso di
segmenti l'ipotenusa del triangolo rettangolo ABC individuato nel mòdano
(vedi ancora Fig. 9).
Fig.
9
Quei costruttori avrebbero potuto dividere l'ipotenusa AC in qualsivoglia numero di
parti uguali: 5, 6...24. Evidentemente dividendola in 6 parti avrebbero ottenuto frazioni pari rispettivamente a 5/6 e 4/6, se divisa in 12 parti, frazioni di 5/12 e 4/12, e così via. La scelta ricadde sul numero 7; numero che
soddisfa le esigenze “fisiche” del dislivello da superare.
Infatti la divisione in 8 parti avrebbe comportato un'alzata di 21,5
cm e una pedata di 30,7 cm (misure che rientrano in quelle
antropometriche ancora oggi usate in alcuni casi); però un'alzata di
21,5 cm x 24 gradini avrebbe superato un dislivello di soli
5,16 m, contro i 5,81 reali. Una divisione in 6 parti avrebbe comportato un'alzata di 28,7 cm e
una pedata di 45,9 cm. Un'alzata di 28,7 cm x 24 gradini avrebbe
superato un dislivello di 6,89 m. Questa suddivisione fu scartata evidentemente, non per
l'eccessivo dislivello superabile, piuttosto per le dimensioni non proprio antropometriche dei gradini.
Il
giusto rapporto tra dimensione dei gradini e dislivello superabile
con un numero fisso e, oserei dire imprescindibile, di gradini: 24, fu
ottenuto dividendo l'ipotenusa in 7 parti uguali.
A prescindere da questi rapporti stringenti tra misure del gradino e la stiba, possiamo dire con tutta sicurezza che nel mòdano sono registrati 6 dati
fondamentali che vennero riportati con i seguenti rapporti numerici:
1, 1/2, 1/3, 1/4, 1/8.
24/24 = 1 →
21 giugno
12/24 = 1/2 →
20 aprile - individuazione della base del 12° anello
8/24 = 1/3 →
20 marzo e 23 settembre
6/24 = 1/4 →
inclinazione della scalinata
3/24 = 1/8 →
21 dicembre
9.
Numeri e solo numeri
Il
mòdano, così come abbiamo ipotizzato fosse concepito, è di per sé
uno strumento dalle proprietà eccellenti, ma forse nasconde ancora
un particolare non di poco conto.
Naturalmente nessuna prova reale
può essere addotta a supporto, per tanto ci accontentiamo delle
ipotesi, basate comunque sulla possibile esperienza pratica che
quelle genti sicuramente avevano.
In
questo capitolo prenderemo in considerazione l'ipotesi costruttiva
del mòdano secondo rapporti numerici ben precisi che potenzialmente
quelle genti avrebbero potuto individuare nelle inclinazioni dei
raggi solari rapportati all'unità di misura scelta.
La
curiosità e l'intraprendenza mi ha portato a valutare quale rapporto
numerico in termini di stibe
possa avvicinarsi ai rapporti numerici riscontrati nel mòdano appena
descritto.
Mi
sono imbattuto in un numero frazionario in base 16 (stibe)
rapportabile anche in base 48 (base sulla quale nel 3° capitolo
abbiamo definito la “unità” di 14,33 cm), seconda la quale in un
triangolo rettangolo avente il cateto verticale pari a 16 stibe o 48
unità, l'inclinazione dei raggi solari al
solstizio d'estate è data da una base pari a 5 stibe o 15 unità,
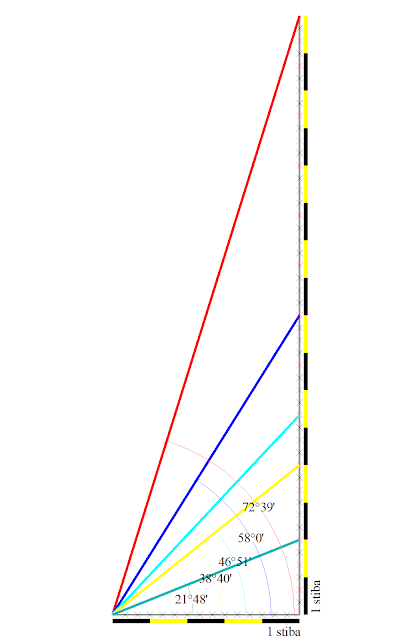
ossia: 5/16 o 15/48 (Fig. 10).
Fig. 10
Secondo
questo rapporto numerico otteniamo un mòdano con inclinazione dei
raggi solari al solstizio d'estate pari a 72°39' che è in ottimo
accordo con l'angolo individuato con altro criterio geometrico per
l'azimut di 154°: angolo di 72°27' e con l'altezza astronomica di 72°17'
(vedi tab. di Fig. 4 del 3° capitolo). In ragione di ciò abbiamo
ricostruito il mòdano, che chiameremo “mòdano
rapportato”,
secondo i numeri frazionati su esposti: 5/16, 1/2, 1/3, 1/4 1/8; ottenendo il seguente risultato:
Solstizio
d'estate modano
rapportato
72°39'4
astronomico 72°17' geometrico 72°27'
20
aprile modano
rapportato
58°00'
astronomico 58°49' geometrico 57°41'
20
marzo modano rapportato
46°51' astronomico 46°30' geometrico 46°30'
21
dicembre modano
rapportato
21°48' astronomico 22°34' geometrico 21°34'
scalinata modano
rapportato
38°40' geometrico 38°44'5
Con
tutta evidenza i valori rientrano in tolleranza, tanto da poter
auspicare che la nostra ipotesi possa risultare vera.
Per
tanto il rapporto numerico da memorizzare per la realizzazione dello "strumento" era 5/16, ossia 5 stibe
di base e 16 stibe
d'altezza, per la costruzione della squadra.
Fatto
ciò, per ottenere le inclinazioni dei raggi solari cercate sarebbe stato necessario dividere il cateto maggiore in 24 parti, per individuare
i noti rapporti intermedi di 3/24 (semplificato in 1/8),
6/24 (1/4),
8/24 (1/3)
e 12/24 (1/2).
A ben vedere però non era necessario neanche questa suddivisione
visto che 1/4 è la metà di 1/2 e 1/8 è la metà di 1/4. Per cui la
divisione del cateto maggiore si risolverebbe memorizzando i seguenti
dati:
Il
cateto maggiore lo divido a metà, il tratto inferiore lo divido
ancora a metà, il tratto inferiore lo divido ancora a metà. Segue
la divisione per 1/3 dell'intero (Fig. 11).
Fig.11
Se
ciò fosse vero, come pensiamo sia, il sistema di costruzione del
pozzo di Santa Cristina in particolare, e forse di qualsiasi altro
monumento in generale, sarebbe svincolato completamente da ogni
successiva verifica dell'inclinazione dei raggi solari e si baserebbe
solo sul modulo della stiba
e dei suoi sottomultipli.
Una
considerazione
Le
elaborazioni da me eseguite sono basate su strumenti di alta
precisione, capaci di scandire i secondi d'arco e i millimetri. Col
programma di grafica si possono impostare approssimazioni
estremamente elevate, che comunque sarebbero ridicole in questo
contesto (lo è già l'approssimazione ai secondi d'arco ed il
millimetro); tenuto anche conto che le approssimazioni da me operate sono
estremamente elevate rispetto a quelle che potevano operare 3000 anni
fa con strumenti primitivi; tanto che gli scarti riscontrati tra
mòdano rapportato
e dato astronomico non sarebbe percepibile. In sostanza se eseguissi
materialmente le costruzioni geometriche descritte, con mezzi che
potremmo definire “di fortuna”; per quanta perizia vi possa profondere, di certo le differenze tra dato teorico e dato empirico non
sarebbero rilevabili.
In
ragione di ciò nel prosieguo dello studio possiamo adottare quale
strumento di misura il mòdano
rapportato.
Seconda considerazione
Da quanto fin qui esposto traspare quello che per quelle genti appariva quale "miracoloso messaggio divino". Un messaggio composto di luce, geometrie e numeri. Luce, geometrie e numeri, che prendevano forma attraverso uno strumento materiale: sa stiba, di qualsivoglia misura scelta e che appunto, essendo slegata da qualsiasi unità campione, era unità di misura assoluta che materializzava numeri assoluti. Numeri assoluti che in qualunque luogo e chiunque, benché di diversa estrazione culturale, che fosse Sardo, Egiziano, Babilonese, Indiano, Cinese se non di qualche antica civiltà precolombiana, avrebbe potuto utilizzare. I rapporti numerici di 1/2, 1/3, 1/4, 1/8 sono assoluti, trascendono da qualsiasi unità di misura e per tanto possono essere usati in tutte le unità di misura. Questa fu la geniale intuizione di quelle genti. E se ciò che andiamo asserendo è vero, nei monumenti di età nuragica non dobbiamo cercare unità di misura particolari, ma numeri e solo numeri.
Note e riferimenti bibliografici