L'uomo, nella sua nudità esprime la condizione di essere umano;
così oggi come nel passato.
Libero da tutti gli orpelli etichettanti il suo modo esteriore d'essere, pensa;
e nel pensare può mentire a se stesso?
L'uomo che pensa deve essere nudo dentro.
Deve essere libero.
12.
Divisione di un segmento in parti uguali
Nei precedenti capitoli abbiamo scritto che la stiba doveva essere divisa in tre parti uguali per poter operare la costruzione degli anelli secondo il procedimento descritto in Fig. 3 (parte 2°). In seguito, nel capitolo 8 abbiamo prospettato l'idea della divisione in 7 parti uguali di un dato segmento per ottenere la giusta dimensione dei gradini della scalinata; mentre nel capitolo 9 abbiamo asserito che il cateto verticale del mòdano doveva essere diviso secondo precisi rapporti numerici pari a 1/2, 1/4, 1/8 e 1/3 dell'intero; infine, nel capitolo 10 abbiamo operato una divisione del raggio di costruzione del cerchio in 9 parti uguali.
A questo punto è necessario dimostrare in modo pratico quale artificio quelle genti utilizzarono per definire in modo esatto un segmento pari ad 1/3 dell’intero, fino ad arrivare a dividerlo in 9 parti uguali. Certamente potremmo andare per tentativi ed arrivare dopo un po’ ad ottenere la misura voluta; però dovendo in seguito operare una divisione di una certa distanza in 9 parti uguali, appunto (vedi capitolo 10 per la divisione del raggio), o 11 parti, come nel caso della costruzione della copertura della scalinata (lo vedremo nel 13° capitolo), è necessario stabilire una regola operativa che possa soddisfare tale esigenza per qualsivoglia numero di parti, pari o dispari che siano.
Potremmo usare un artificio del tutto empirico
consistente, nel caso della divisione della stiba in 3 parti uguali,
nel prende una funicella lunga 43 cm e piegarla in tre parti con un
semplice metodo. Tenendo un capo della funicella tra indice e pollice
di una mano e l’altro capo con indice e pollice dell’altra mano,
si fa scorrere fino alla tensione della funicella, accavallandola sui
due indici. In questo modo si ottiene un segmento di 14.33 cm. Lo
stesso metodo possiamo utilizzarlo per dividere una qualsiasi
lunghezza in più parti sia pari che dispari, accavallando
più spire attorno ai due indici. E' un metodo empirico la cui precisione è demandata alla scrupolosa attenzione dell'operatore; ma per quanto si possa essere certosini, le pieghe della corda "rubano" lunghezza. Forse il metodo usato fu proprio questo, però c’è un metodo geometrico
affidabilissimo tanto semplice e veloce nel suo utilizzo, quanto
precisissimo nel risultato, che necessita di osservazione, intuito e neuroni ben allenati; doti che di certo non mancavano a quelle genti.
Quanto andremo a spiegare potrebbe provare in modo
significativo che quelle genti, benché in modo del tutto pratico e
forse inconsapevole, utilizzavano una variante del teorema di Talete
allo scopo di dividere un qualsivoglia segmento in parti uguali di
qualsivoglia rapporto numerico e qualsivoglia triangolo (non
è necessario utilizzare il triangolo rettangolo. Qui lo abbiamo
usato per comodità esplicativa).
Partiamo naturalmente dall'iniziale intuizione che
sinteticamente descriviamo nelle sue fasi secondo le immagini di Fig. 17a, 17b, 17c, 17d; tenendo conto del fatto che la peculiarità qui descritta valeva per
la latitudine Santa Cristina nel 1000 a.C., come abbiamo già detto
in nota 5 del
capito 7 .
Fig. 17d
Studiando le ombre proiettate da una pertica infissa
al suolo, per un medesimo angolo azimutale di due momenti cardine del
ciclo solare – solstizio d'estate ed equinozi - una mente scaltra e
curiosa, abituata all'osservazione poteva cogliere con facilità il
rapporto intercorrente tra la lunghezza delle ombre proiettare agli
equinozi e ai solstizi. Le immagini di Fig. 17 mostrano gli ipotetici
passaggi procedurali che portarono alla scoperta.
Siamo
persuasi del fatto che il rapporto intercorrente tra i diversi spessori degli anelli della tholos sia stato stabilito in seguito a questa
scoperta. In ragione di ciò possiamo avanzare l'ipotesi che la
suddivisione de “sa
stiba”
in 3 parti uguali sia diretta conseguenza di questo rapporto
astronomico.
Descriveremo al presente un metodo.
Registriamo l'ombra proiettata da una pertica alta AB, il 21 di giugno
all'azimut di 153° (Fig.17a). In seguito misuriamo l'ombra che proietta lo stesso bastone
verticale all'equinozio di autunno (Fig.17b). Il raffronto tra le due lunghezze
dimostra che l'ombra agli equinozi è esattamente 3 volte la prima
misura.
Successivamente si può verificare che l'ombra
proiettata il 21 di dicembre è 8 volte la misura dell'ombra al 21di giugno.
Osservando ancora le immagini delle Figg. 17c e 17d, sorge
spontaneo l'interrogativo che si pose l'ipotetico studioso di 3000
anni fa. Quanto deve essere alto il bastone infisso a terra per avere
all'equinozio la stessa lunghezza dell'ombra al solstizio d'estate?
Evidentemente la domanda prelude un percorso logico: se il bastone di
uguale lunghezza determina agli equinozi un'ombra tripla di quella
del solstizio d'estate, per ottenere ombre di uguale lunghezza il
bastone “dovrebbe” essere alto 1/3. Con tutta evidenza la
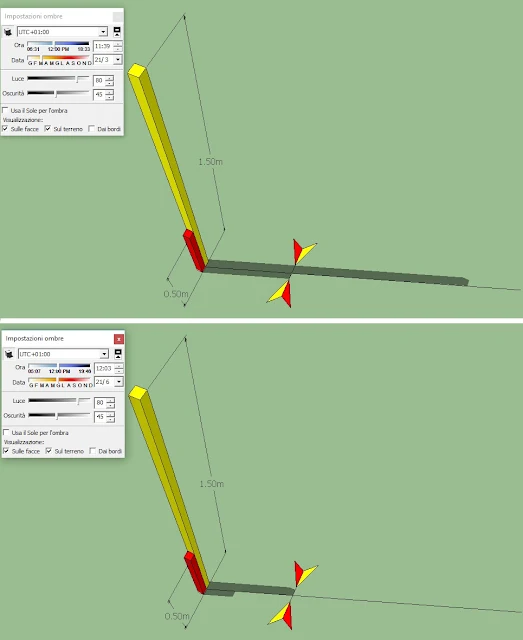
verifica si effettua ancora con le ombre proiettate (Fig. 18).
Fig.
18
Simulazione
in 3D eseguita con Google SketchUp1
In sostanza si affianca al bastone già infisso un
secondo bastone alto 1/3 del primo. Il giorno dell'equinozio si
registra la lunghezza dell'ombra proiettata dal bastone più corto al
passaggio del sole per l'azimut prescelto, apponendo un segno
all'estremità dell'ombra. In seguito, il giorno del solstizio
d'estate si verifica la lunghezza dell'ombra quando il sole passa per
il medesimo azimut. Il metodo empirico non necessita di alcuna
elaborazione teorica, né costruzioni ad hoc di carattere geometrico;
queste vennero realizzate in seguito, quando si capì la potenzialità
del metodo, che poteva essere usato per dividere un segmento di
qualsivoglia lunghezza in un numero di parti uguali dettato dalle
esigenze del momento.
In termini geometrici possiamo dire che moltiplicando
per “n” unità la misura AC, il tratto “ennesimo” intercetta
l'ipotenusa NB del triangolo ABN in un punto che è 1/n di AB. La
soluzione geometrica è molto più facile e intuitiva di quanto possa
una spiegazione teorica, per tanto proponiamo l'immagine esplicativa
di Fig. 19.
Fig.
19
Con questa costruzione geometrica è possibile
dividere un qualsiasi segmento in “n” parti, ottenendo la misura
esatta della parte cercata.
Con molta probabilità fu questo il metodo utilizzato
da quegli architetti astronomi e non vi è alcun motivo di carattere
intellettivo che possano far ritenere falsa questa ipotesi 3000 anni
fa, perché l'approccio al problema è semplicemente osservativo e
comparativo; e menti scaltre capaci di costruire figure geometriche
complesse come l'ovale e l'ovoide; che erano in possesso del
principio statico dell'arco a conci, prima e dell'arco orizzontale
(tholos), dopo; nonché capaci di architetture di luce diretta e
riflessa, di certo non avevano alcun problema a manipolare dati come
quelli qui esposti. Eratostene di Mileto quando calcolò il diametro
della Terra 800 anni dopo i costruttori del pozzo sacro, non aveva
alcuno strumento se non le ombre generate dal sole e una grande mente
deduttiva.
13.
Ombra e penombra: quale dilemma!
Sembrerebbe
di poco conto stabilire il limite di demarcazione di un'ombra
proiettata dal sole, ma non è così; almeno nel caso in cui si
voglia definire con una certa precisione tale limite. Infatti
osserviamo che le ombre portate dal sole in genere non sono nette per
il fatto che l'astro non è una sorgente puntiforme; per tanto i
bordi sfumano sempre nella penombra. Penombra che si fa sempre più
ampia tanto più lontano dal piano di proiezione è l'oggetto che
produce l'ombra. Per tanto se prendiamo in considerazione il caso di
Fig. 18, ci rendiamo conto che l'ombra proiettata dalla pertica più
alta è certamente meno nitida di quella più corta, e se dobbiamo
delimitare il confine di quella prima ombra, lo facciamo con un certo
grado di incertezza rispetto alla seconda, più nitida.
Il
problema si risolve in modo alquanto semplice, posizionando in
corrispondenza di quel bordo dove ombra e penombra segnano un
continuo sfumato indistinguibile, un qualsiasi oggetto vicinissimo al
piano di proiezione, tanto vicino che la penombra di questo di fatto
non esiste. L'accostamento individua un bordo netto
dell'ombra rispetto alla penombra, tale da poter stabilire il
confine in modo precisissimo.
Note e riferimenti bibliografici
1 Non potendo col programma SketchUp proporre la situazione
astronomica di epoche passate, la simulazione è stata condotta
ponendo l'oggetto alla latitudine di Palermo per dimostrare ciò che
avveniva alla latitudine di Santa Cristina nel 1000 a.C.. Vedi nota 5 della parte 3°.







Nessun commento:
Posta un commento